Materials

• Cubes having an edge length of at least 2 inches (1 per student)
• Dot paper
• Protractor
• Compass
• Axonometry Overhead
• Axonometry Activity Sheet 1
• Axonometry Answer Key 1
• Axonometry Activity Sheet 2
• Axonometry Answer Key 2

Instructional Plan

For this lesson, students must be familiar with graphing complex numbers in the complex plane and operations with complex numbers.

In the first period, distribute a cube to each student. If you do not have cubes, then have students make their own origami cubes (instructions on how to do this can be found doing a simple search on the internet). Have them observe the cube from different points of view. Next, have students sketch, as best they can, their cube on a piece of dot paper from the perspective of one vertex being closer to them than the others, and so that the three edges (whose common endpoint is the vertex closest to them) appear to be the same length.

Then show the Axonometry Overhead.

 Axonometry Overhead 

Ask students, "Without measuring, do the three edges that meet at the vertex closest to you appear to be the same length?" [Yes.] Have students hold their cube in front of them, using the same perspective as in the overhead. Then ask them to slightly tilt their cube, so that point A moves away from them and points B and C move closer to them. Ask, "When you tilt the cube, does the appearance of the edge lengths change?" The answer should be yes. If students aren't seeing that one of the edges appears to decrease in length and two of the edges appear to increase in length, have them increase the tilt of the cubes until they can see it. This is a central idea of the lesson. Then ask, "Do the angles between the same three edges appear to change as you tilt the cube?" [Yes.] This is a secondary idea of the lesson. Ask, "Why don't the lengths of the edges actually change?" [The lengths of the edges do not change because the physical shape of the cube is not changing. The edge lengths are constant.] Now say, "We are going to mathematically explore the relationship of the three edges that meet at the vertex closest to you."

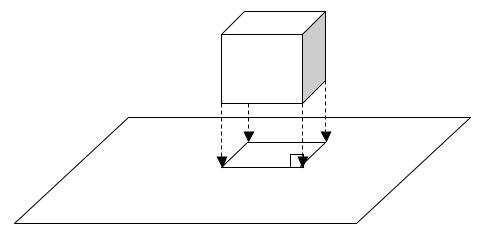
Explain to students that the drawings of cubes we are dealing with in this activity are the result of a 3-dimensional cube being projected straight down onto a 2-dimensional plane at a 90-degree angle. This is the same type of projection that happens with an overhead projector and it is called an orthogonal projection.

The mathematician Gauss realized that it is very useful to project the 3-dimensional figure onto a complex plane. A complex plane has one real axis and one imaginary axis. A point on the complex plane is defined by its coordinates, which represent a complex number. For example, the coordinate (2, 3) represents the complex number 2 + 3i. In three dimensions, a cube can be fully specified by the coordinates of one vertex and the three nearest vertices. When these three vertices are projected onto a complex plane, the corresponding vertices in the projection can be represented by the complex numbers A, B, and C. Gauss’s Fundamental Theorem of Axonometry states that if A² + B² + C² = 0, then the drawing on your paper is an orthogonal projection of a 3-dimensional cube above the paper. In other words, it is a good representation of a cube.

To understand why Gauss’ theorem is true, you can show that perpendicular vectors of the same length can be generated in a complex plane by multiplication by i. So, for example, start with a vector defined by point A at (3, 4i). The vector is defined with its tail at the origin. Multiplying the coordinates of A by i gives 3i and 4i² = –4. This defines a new vector with point B located at (–4, 3i). Students can try this with different points and they will always find:

1. The length (magnitude) of the vector for A equals the length (magnitude) of the vector for B. The transformation does not change the length (magnitude) because multiplying by i is similar in some regards to multiplying the identity element by 1.
2. The vector for A is always orthogonal to the vector for B.

Next, you can show that for any two points generated this way, A² + B² = 0. For the points above, A² = (3 + 4i)²= 9 + 24i - 16 and  B² = (–4 + 3i)² = 16 – 24i - 9. It is easy to show that these squares will always generate three sets of opposites that sum to 0. In this case:

            3² and 3i ²

            –4² and 4i ²

            24i and –24i

The general algebraic case goes as follows:

Assume A is located at (x, yi). Then B, found by multiplying A's coordinates by i, is located at (-y, xi). A²=x²+2xyi-y² and B²=y²-2xyi-x². From here, it is easily shown that A² + B² = 0.

Next, apply this analysis to the cube itself. Each face of the cube can be plotted in a complex plane. For any two vertices that define orthogonal edges of the cube, A² + B² = 0. It is easy to show that for three vertices that define the cube (all neighbors of a single vertex), A² + B² + C² = 0 because A² + ² = 0 and B² + C² = 0.

Return now to the orthogonal projection. In this lesson, students will observe that the coordinates a and b in the orthogonal projection generally do NOT define orthogonal vectors. The coordinates in the projection are orthogonal only when the complex plane chosen is parallel to one of the cube’s faces. However, part of the genius in Gauss’s theorem is that we still benefit, because properties of the 3-dimensional relationship still hold with the 2-dimensional analog. The full proof is too long for this lesson, but in a nutshell, A² + B² + C² = 0 even when A² + B² ≠ 0 and B² + C² ≠ 0 in two dimensions.

A key point to emphasize with students is that Gauss’s theorem holds only when the vectors of the 3-dimensional figure meet two criteria:  they have the same length (always true for a cube) and they are orthogonal (always true for a cube). So, if the 3-dimensional figure is not a cube, then a² + b² + c² ≠ 0.

Explain that students will evaluate the formula for the complex numbers that represent the endpoints—A, B, and C—of the generating line segments. If a² + b² + c² = 0, then the 2-dimensional drawing is an accurate representation of the 3-dimensional cube. Distribute the Axonometry Activity Sheet 1.

 Axonometry Activity Sheet 1

 Axonometry Answer Key 1 

Ask students to work in pairs as they complete the activity sheet. Tell them to refer to the overhead to help with the visualization described in the activity sheet.

Afterwards, hand out Axonometry Activity Sheet 2 to each student.

 Axonometry Activity Sheet 2 

 Axonometry Answer Key 2

Circulate as students work on the activity sheet. Remind them to use their cubes to help them visualize the actions described in the activity sheet. The easiest way to find another set of points would be to extend the three edges of a cube made by the points in Question 1 by a constant factor (ex: double the lengths of all the edges).

When students have completed the activity sheet, have them share their answers with the class. Guide the discussion around the conservation of the total length of the three edges as the cube is tilted, and the angle relationships between the edges as the cube is tilted. Ask, "Why are the angle measures of the projection's edges greater than the angle measures of the actual cube?" [The perspective of the projected cube causes the angles of the projection to be greater in size than the angles of the actual cube.] Students might also think that because the actual edge lengths of a cube do not change, then the projection's edge lengths also should not change. Explain that, according to how the cube is tilted, the projection will cause some edges to shorten while others lengthen. However, the total length of the projection's edges should not change.

End the class with a summary of the discussion. Ask students, "Where in a real-world context might a 3-dimensional cube be represented 2-dimensionally? " [Answers may vary from blueprints to technical drawings.]

As the final activity, have students suppose they will create three points in which a² + b² + c² is close to, but not exactly, zero. Have students explain what this would mean in terms of the lengths of the line segments. [They are all close to each other in length.] Ask them if one of the points can be moved so that a² + b² + c²  = 0. Encourage students to conclude that the reason a² + b² + c²  = 0 for a cube is because cubes have equal edge lengths.

Reference 

Assessments and Extensions

Assessment Options

1. Use Gauss' theorem to see if the points A(3, 6), B(2, –3) and C(6, –2) generate a cube. Then look for a pattern in the coordinates of these points. Use the pattern to generate other numbers that also the pattern always work?
2. Give students the following 3 points: A(–55, 148i), B(51, 94i), and C(160, 20i). Have students create a graph of their "cube" based on these three points. Does the picture seem like an accurate representation? Now have them calculate a² + b² + c². Is the answer "close" to zero? Discuss what "close to" mean in terms of complex numbers.

Extensions

1. Have students find an example of a cube in a magazine or printed from a Web page. Ask them to attach it to a complex grid on graph paper and write down the three generating points, a, b, and c. (They may need to enlarge the image with a photocopier to have better accuracy.) Have them use the a² + b² + c² = 0 formula to check the reasonableness of the representation.
2. Have students research the use of projections in technology, especially in computer animation. Have students discuss how 3-dimensional objects are represented 2-dimensionally, and how mathematics is involved in computer animation.
3. Have student explore where a² + b² + c² is less than or greater than zero.  Have students create three points where a² + b² + c² > 0  and three points where a² + b² + c² < 0. Have them explain what these values mean in terms of a rectangular prism projected upon a page. [It means that the object being projected is not a good representation of a cube.]

Questions and Reflections

Questions for Students

1.What happens to a vector in the complex plane when it coordinates are multiplied by i?

[A new vector of the same magnitude is created and it is perpendicular or orthogonal to the original vector.]

2. What is the difference between drawing a box (or a rectangular prism) and drawing an actual cube?

[A cube is a type of rectangular prism with congruent edges and faces while other rectangular prisms don't have to meet these criteria. Any axonometry drawing on paper that is supposed to be an actual cube should somehow show that the edges and faces are congruent.]

3. What are the similarities and differences between squaring a complex number such as 2 + 3i and a binomial?

[The binomial 3x + 2 can be written 2 + 3x. When you square the binomial, you get 9x² + 12x + 4. When you square the complex number you get 9i² + 12i + 4 = 9(–1) + 12i + 4 = –9 + 12i + 4 = –5 + 12i. They may look different, but a complex number is a binomial, so squaring a complex number is the same thing as squaring a binomial.]

4. Ask students to state some patterns they noticed in the course of the activities.

[Answers will vary but students should note that when C is located on the imaginary axis, A and B are symmetric about the imaginary axis.]

Teacher Reflection

• How did students demonstrate that they understood the big picture of applying operations on complex numbers to understanding a particular geometric problem?
• In what ways did students seem motivated by this activity to want to explore and ask questions about complex numbers, art, or both? If students did not seem motivated, what could you have done differently?

Objectives and Standards

Students will:

• Draw representations of cubes using 3 generating line segments.
• Learn about spatial geometry by drawing different views of a cube.
• Plot complex numbers in the complex plane.
• Multiply complex numbers.

Related Resources