Tempted by Triangles
How many different triangles are in the figure below?

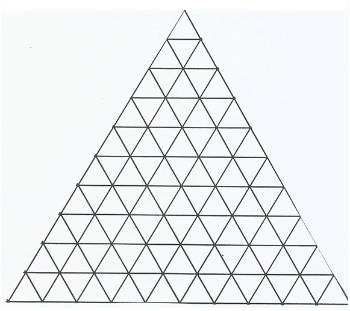
Extension: Note that this is a 10 by 10 by 10 triangular grid.
What if it were an N by N by N triangular grid, then how many triangles?

More Ponderings: 

One approach to counting all the triangles in the 10 x 10 x 10 grid of triangles is to start with a smaller problem. For instance, if we start with a 4 x 4 x 4 grid, we see that there are triangles of different sizes in the grid. For example, there are 1 x 1 x 1 triangles in rows that “‘point up,” and each successive row has one more triangle than the previous row, as shown by the red triangles in the drawings below:

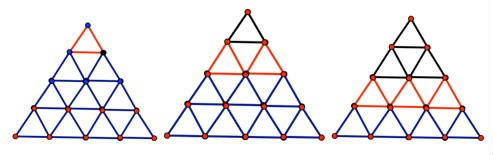  , and so on.

There are 1 + 2 + 3 + 4, or 10, such upward pointing triangles of edge length 1 in a 4 x 4 x 4 triangular grid. In the case of our 10 x 10 x 10 grid, there are 1 + 2 + … + 10, or 55, “upward pointing” triangles of edge length 1.

Then we can see that there are upward pointing triangles of other sizes: 2 x 2 x 2 triangles, 3 x 3 x 3 triangles, and so on, all the way up to the one large 10 x 10 x 10 triangle itself. I have seen students cut out triangles of the various sizes and move them into position to count the number of triangles of a particular size. In the same way, we could cut out and move the red triangle of edge length 2 to the different possible positions to see that there are 1 + 2 + 3, or 6, of these triangles in the 4 x 4 x 4 grid.

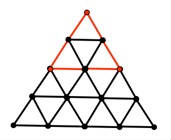
For the 10 x 10 x 10 grid, we can see that there will be 1 + 2 + 3 + … + 9, or 45, upward pointing triangles of edge length 2. In a similar way, we can find—

1 + 2 + . . . + 8 = 36 upward pointing triangles of edge length 3,

1 + 2 + . . . + 7 = 28 upward pointing triangles of edge length 4, and so on,

continuing down to

1 + 2 = 3 upward pointing triangles of edge length 9, and

1 upward pointing triangle of edge length 10.

Altogether, there are 55 + 45 + 36 + 28 + 21 + 15 + 10 + 6 + 3 + 1, or 220, upward pointing triangles of all sizes in the grid.

Students may notice that this solution involves sums of the triangular numbers. In fact, there are many wonderful patterns in the Tempting Triangles problem!

Of course, this is only part of the answer, because there are also “downward pointing” triangles in the grid! In the case of the 4 x 4 x 4 grid, there are 1 + 2 + 3, or 6 downward pointing triangles of edge length 1. But notice that there is just 1 downward pointing triangle of edge length 2, so watch for something different when counting the rest of the downward pointing triangles.

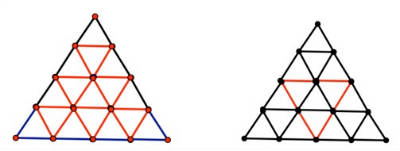
More ponderings on this problem, and the solution for the general case for the number of triangles in an N x N x Ntriangular grid, will appear in subsequent columns.

More Ponderings:

Last month we saw that in our Tempting Trianglesproblem there are a variety of sizes of triangles, that some triangles “point up” and some “point down,” and that the pattern for the upward pointing triangles is related to sums of triangular numbers. For a 10 x 10 x 10 grid of equilateral triangles, there are 55 + 45 + 36 + 28 + 21 + 15 + 10 + 6 + 3 + 1 = 220 upward pointing triangles of all sizes in the grid. There are 55 of the 1 x 1 x 1 equilateral triangles, 45 of the 2 x 2 x 2’s, and so on, all the way down to the 1 big equilateral triangle itself.

However, the downward pointing triangles follow a different pattern. For example, in the 8 x 8 x 8 grid shown below, there are only 7 downward pointing 1 x 1 x 1 triangles on the bottom row (although there are 8 upward pointing triangles in the bottom row), so there are 7 + 6 + 5 + 4 + 3 + 2 + 1 = 28 downward pointing 1 x 1 x 1 triangles in this 8 x 8 x 8 grid. Also, notice that there are only 5 downward pointing 2 x 2 x 2 triangles with a vertex on the bottom edge (numbered in the figure below) of the 8 x 8 x 8 grid. As we move up a row at a time, we see there will be 5 + 4 + 3 + 2 + 1 = 15 downward pointing 2 x 2 x 2 triangles, and 3 + 2 + 1 = 6 downward pointing 3 x 3 x 3 triangles, and just 1 downward pointing 4 x 4 x 4 triangle. Also, we observe that a 4 x 4 x 4 triangle is the largest sized downward pointing triangle that we can obtain in an 8 x 8 x 8 grid—there are no downward pointing 5 x 5 x 5 triangles that will fit in this  grid.

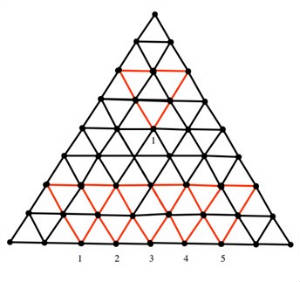
Thus, the pattern for the total number of downward triangles also involves sums of triangular numbers, but only every othertriangular number. There are 28 + 15 + 6 + 1 = 50 downward pointing triangles of all sizes in the 8 ´ 8 ´ 8 grid. And so, for our original 10 x 10 x 10 grid, the total number of downward pointing triangles will be the sum of the 9th, 7th, 5th, 3rd, and 1st triangular numbers, respectively, or, 45 + 28 + 15 + 6 + 1 = 95.

The total number of all triangles of all sizes in the 10 x 10 x 10 grid is thus 220 + 95 = 315.

For an n x n x n grid, the total number of upward triangles will be the sum of the first ntriangular numbers, whereas the total number of downward triangles the sum depends on the parity of the original triangular grid—that is, whether it is even or odd. “To obtain the total number of downward triangles, we start with the (n– 1)st triangular number, and form the sum of triangular numbers (n – 1)st + (n – 3)rd + (n – 5)th + …, continuing in this way down to 1, or 3, as the final summand.”

The ultimate challenge here is this: can you find a closed-form formula for the number of triangles in an n x n x ngrid? Or to put it another way, can you find a formula for the sum of the firstn triangular numbers? You’ll at least need that! Ponder away!