Circling Around
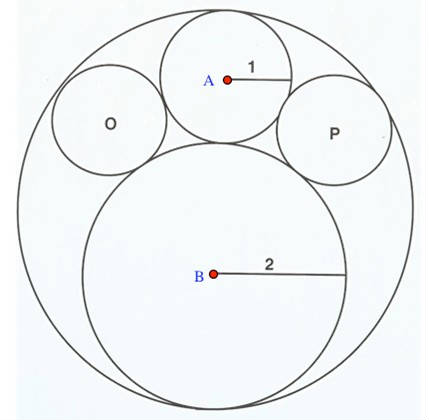
Suppose that the circles in the figure below are tangent to one another. The radius of the circle centered at A is one unit, and the radius of the circle centered at B is two units. What are the radii of the circles centered at O and P?
Some Ponderings:
The May Problem to Ponder asked what the radius of the two congruent circles O and P is, given that circle A has a radius of 1, circle B has a radius of 2, and that circles O and P are mutually tangent to circle A, circle B, and the surrounding circle.
The surrounding circle therefore has a radius of 3.

One approach that students often take is to start connecting centers of the circles, as in the figure below. This might be a fruitful approach to finding relationships. Triangle ADB is formed from the centers of circles that are tangent to one another, so segments AD, AB, and BD pass through the points of tangency. For example, points I and J are two such points. Similarly, the line passing through the centers C and D of the circle of radius 3 and the circle whose radius is (as yet) unknown passes through the point L of mutual tangency of those two circles.
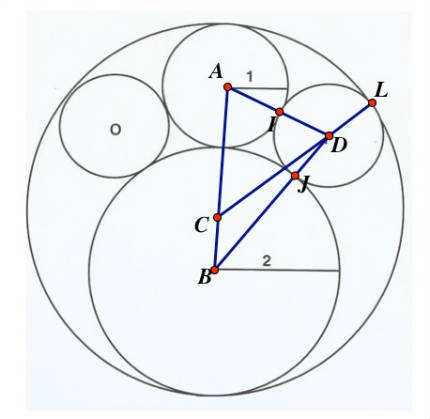
We now have a number of triangles in the figure and can begin to look for relationships among them, as well as representations for the lengths of their sides. In my experience, many students will embed this diagram in a coordinate plane and try to use a lot of analytic geometry
to find lengths of sides, coordinates of centers from intersecting lines, and so on. Or they might try to use some trigonometry and relationships between the sides. Both these approaches can be a tad laborious.
If one is going to try trigonometry, looking for some right triangles, or creating some, might be helpful.
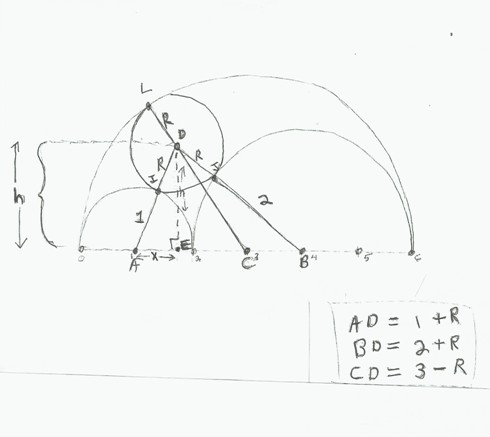
Suppose that we drop an altitude h from point D to segment AB, and label the intersection of h with AB as point E. Now we have some promising possibilities to investigate for relationships, because we have right triangles all over the place!
In the sketch below based on some student work, R is the unknown radius of the mutually tangent circle, and x is the length of segment AE. We’ll return to more pondering on the radius of that circle next month.
Further Ponderings:
Last month we concluded our discussion of the problem Circling Around with the student-submitted diagram below. Recall that we are trying to find the radius R of the circle that is mutually tangent to the three circles of radii 1, 2, and 3 units, centered at points A, B, and C, respectively. Altitude h (segment DE) is dropped from the center, D, of the unknown circle to point E on segment AB. All three centers of the known circles lie on AB. If we let x be the length of segment AE, we can form three right triangles: ADE, BDE, and CDE.

We can therefore set up a system of three equations in the three unknowns, x, h, and R, where R is the radius of the unknown circle:
- h2 + x2 = (1 + R)2
- h2 + (3 – x)2 = (2 + R)2
- h2 + (2 – x)2 = (3 – R)2
As we do the algebra, the quadratic terms nicely drop out, and we find that
(Equation 1) – (Equation 2) => –9 + 6x = –3 – 2R (Let’s call this Equation 1’)
(Equation 2) – (Equation 3) => 5 – 2x = –5 + 10R (Let’s call this Equation 2’)
Then (Equation 1’) + 3 x (Equation 2’) => 6 = –18 + 28R
24 = 28R, so R = 24/28 = 6/7 !!!!
Did you think it was going to be a rational length? Tell the truth now…
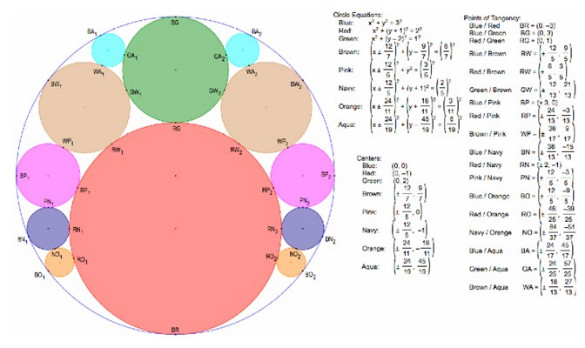
Here is a beautiful rendition of an extension of the Circling Around problem, sent in by Peggy House and shared with her permission. In Peggy’s figure, the blue circle is the outside circle of radius 3; the red circle is the circle of radius 2, the green circle is the circle of
radius 1, and the brown circle is the cotangent circle from our original problem. Then Peggy’s pink circle is the next cotangent circle in the pattern, and so forth for her circles in other colors.
Surprising results, eh?