The Common Core State Standards for Mathematics (CCSSM) do not make any promises about the teaching practices that should be used to support students’ enactment of the standards. Thus, equity gets framed as achievable through making the standards a goal for all students. We know from research on past reform efforts that standards without explicit (or companion) teaching practices, and teaching practices without explicit attention to equity, will inevitably result in the failure of the standards to achieve goals for students. This commentary provides a framework for future research that hypothesizes research-based equitable mathematics teaching practices in support of the CCSSM’s Standards for Mathematical Practice, connecting research, policy, and practice in order to realize the equity potential of the CCSSM.
Key words: Equity; Diversity; Special needs; Common Core State Standards for Mathematics; Equitable teaching practices; Research issues
The Common Core State Standards for Mathematics (CCSSM) delineate the mathematical content all students should learn as well as eight Standards for Mathematical Practice (SMP) through which students should engage the mathematical content (National Governors Association [NGA] Center for Best Practices & Council of Chief State School Officers [CCSSO], 2010). In this commentary, we consider how the CCSSM, and thus the SMP, is positioned within a larger political context and how these political forces, combined with a lack of attention to equity, will likely serve to reify existing inequities in mathematics learning. We focus on the enactment of the SMP as a way to make the CCSSM more equitable and offer a framework for future research linking equitable teaching with the SMP.
Although a few states that initially adopted the CCSSM have recently withdrawn and a few more states are reviewing their position (Bidwell, 2014), as of August 2015, 42 states have adopted the CCSSM (Ujifusa, 2015). Moreover, the National Council of Teachers of Mathematics (NCTM) has expressed support for the opportunity the CCSSM provides (http://www.nctm.org/CCSSMposition/) and produced resources aimed at supporting teachers’ understanding of the CCSSM and the SMP (e.g., Koestler, Felton, Bieda, & Otten, 2013). These efforts point to the instantiation of educational policy through what may be the “most profound and widely distributed educational reform activity in recent history” (Koestler et al., 2013, p. v).
States opting out of the CCSSM and the ongoing debate about the policy, even as efforts are made to support its instantiation, reflect the fact that the CCSSM, like education more generally, is situated within broader sociopolitical structures and systems of privilege and oppression that influence how such policies are framed and taken up (Herbel-Eisenmann et al., 2013). Consideration of these broader sociopolitical structures is imperative, however, if the efforts of the CCSSM are to move beyond rhetoric toward change in students’ learning of mathematics (Apple, 1992; Gates & Vistro-Yu, 2003).
The CCSSM is situated within broader social and political contexts and narratives. As such, it can be taken up and instituted in various ways. As outlined by Martin (2013, p. 318), a number of scholars (e.g., Apple, 1992, 2000; Atweh & Clarkson, 2001; Atweh et al. 2008; Ernest, 2009; Gutstein, 2008, 2009) have provided “compelling evidence” that mathematics education (which includes the CCSSM), when considered in relation to “market forces, market-driven goals, and increased globalization,” is positioned as part of a larger, neoliberal narrative disconnected from the experiences and realities of students from nondominant communities (Eppley, 2015; Gutstein, 2010).
Neoliberalism supports the privatization of social goods and competitive markets as opposed to government provisions related to housing, health care, and education. The neoliberal agenda includes a focus on economic well-being and competitiveness in a global economy (Woodrow, 2003) and reflects a shift from education as a social concern to education as a market concern (Eppley, 2015). Neoliberalism focuses on cultivating citizens for gainful employment, as opposed to contributing to democratic life. As such, it contradicts a focus on students’ communities, beliefs, and points of view and is grounded in racist ideologies (Lipman, 2012). Skovsmose and Valero (2002) argue that this reflects a “paradox of inclusion” because there is an inherent contradiction between the discourse of the neoliberal agenda—that of inclusion, well-being, and universal access tied to globalization of the economy—“and the deep disempowerment and exclusion that certain social sectors actually experience as a result of the practices associated to that discourse” (p. 384). The existence of this paradox directly challenges efforts toward equity and justice. Policies reflecting a neoliberal agenda have been shown not to reduce inequity (and perhaps exacerbate inequity) (Diversity in Mathematics Education [DiME] Center for Learning and Teaching, 2007; Eppley, 2015; Gutstein, 2010; Skovsmose & Valero, 2002). As we outline next, the maintenance (or exacerbation) of inequity can occur through lack of attention to particular issues in the policy document itself as well as within the interpretation and subsequent implementation of the policy.
Further, the CCSSM lacks an explicit focus on race, class, and gender (Gutstein, 2010) despite the fact that “institutional and structural racism and political economy loom large in the experiences of urban youth, both within and outside the mathematics classroom” (Gutstein, 2010, p. 16). The absence of such focus or so-called “e(race)ing” suggests that the CCSSM, too, may reflect “white institutional space” (Martin, 2008, p. 387) that will continue to marginalize the lives and experiences of students from nondominant communities. As seen with California’s Algebra for All policy enactment, inattention to equity, race, and power leaves beliefs, conceptions, labels, and discourses about students from nondominant communities unchanged and suggests a need to “develop meaningful interventions, inside and outside of school, to empower marginalized students with mathematics so that they can change the conditions that contribute to inequities” (DiME Center for Learning and Teaching, 2007, p. 426).
Together, these arguments suggest that the CCSSM, with its implicit political and economic goals and its lack of explicit attention to race, gender, class, and so forth, is not framed to support equity. Further complicating this issue is the fact that the CCSSM does not provide, nor was it intended to provide, a description of specific pedagogical practices that can support student learning of its content goals and practices of engagement. That is, the connection between policy and practice is left undefined in the CCSSM. Past policy efforts suggest that a specific focus on mathematics teaching practices is essential for success. In the Chicago Public Schools’ College Preparatory Curriculum for All initiative, for example, although the policy ending remedial classes was implemented quickly and schools successfully eliminated low-level course work previously common among students labeled as “low ability,” virtually no change occurred in failure rates, test scores, or the likelihood of students entering college (Allensworth, Nomi, Montgomery, & Lee, 2009). These researchers concluded that a focus was needed on how content and curriculum were taught and, in particular, how to teach the content to different types of students. Similarly, Cuban (1990) argued that the reason reform happens “again, again, and again” is related to “the decoupling of instruction from administration and policymaking” (p. 11). One reason such policy may not have been successful is because systems of privilege and oppression operate in such a way that structures of schooling embedded in teaching practices were not affected (Apple, 1999). Rather, policies are taken up so as to “reinforce things as they are or to tinker with innovations that will leave untouched the regularities [and inequities] of schooling” (Cuban, 1990, p. 10).
Given the role that the CCSSM may play in perpetuating inequity, it is imperative to consider how this process may be co-opted to make its implementation more equitable. Research exists that can inform the identification of effective, equitable pedagogical practices that support students’ learning of mathematics, which we refer to as equitable mathematics teaching practices. In this commentary, we suggest a framework for future research that hypothesizes research-based equitable mathematics teaching practices in support of the SMP. We argue that making a connection to both equitable mathematics teaching practices and the SMP can inform directions for related mathematics education research. We found that it made sense to align equitable mathematics teaching practices with the mathematical practices students would engage with; thus, we focus on the enactment of the SMP as a way to make the CCSSM more equitable. The SMP include eight “varieties of expertise that mathematics educators at all levels should seek to develop in their students” (NGA & CCSSO, 2010, p. 6). In identifying equitable mathematical teaching practices that map to the SMP, we started with those ideas outlined in the chapter on culture, race, and power in the Second Handbook of Research on Mathematics Teaching and Learning (DiME Center for Learning and Teaching, 2007) and added more from recent research. Importantly, we recognize that the list of practices we offer is necessarily an incomplete list.
As Cuban (1990) notes, “we can do better” (p. 12) than reform “again and again” (p. 11) by gathering data on the history of particular reforms in specific contexts (e.g., classrooms, schools, districts), as situated within broader structures influencing this work (e.g., school, structures, curricula), and by “examining carefully the alternative explanations offered” (p. 12). To do this, we suggest that mathematics education researchers conduct studies to help co-opt the CCSSM toward equity, including those that examine connections between equitable mathematics teaching practices and the SMP. Research aimed toward promoting equity requires the study of these reforms in specific contexts, such as classrooms, schools, and districts, in order to understand how such reforms occur within inequitable structures and how they do and do not support each student’s learning of mathematics. We align equitable mathematics teaching practices with the SMP, connecting goals for students with research on effective pedagogy for students from nondominant communities. Using this as a framework, we call for specific research that will allow the field “to adopt a more informed stance when dealing with the contentious issues of policy and practice” (Kilpatrick, 2007, p. 107).
A Framework for Linking Equitable Mathematics Teaching Practices to the SMP
In an effort to provide some guidelines for thinking about how teachers might provide equitable opportunities for students as they engage in the SMP, we identified what we considered to be some of the core equitable mathematics teaching practices and the research that supports those practices. In Table 1, we articulate the equitable mathematics teaching practices that we have identified and provide selected examples of how each practice might be enacted. We recognize that this is not a complete review of the literature, but we want to provide a starting point to engage the field in a conversation about the practices and to encourage research on these ideas as they are connected to the SMP. We also acknowledge that the constraints of a research commentary necessarily limit our ability to address other aspects that have been found to inform equitable teaching practices; some of those not incorporated in our discussion include teacher positionality (e.g., Hand, 2012; Wager, 2014), identity (Esmonde, 2009), and teacher beliefs (e.g., Philipp, 2007).
After identifying the equitable mathematics teaching practices, we identified examples of how each practice might be enacted in supporting students to develop each of the SMP. Imagine, for example, a table in which the equitable mathematics teaching practices from Table 1 are listed in column 1 and the SMP are listed in columns 2 through 9, such that sample practices at the intersection of each equitable mathematics teaching practice with each SMP are delineated (see Figure 1). We do not have the space here to elaborate practices for the intersections represented by each cell in the table; however, in an effort to illustrate the possibilities of such a framework, we provide examples of practices that would populate two cells in such a table.
Table 1 Equitable Mathematics Teaching Practices| Equitable practice | Examples of the practice |
| 1. Draw on students’ funds of knowledge | Build on community and cultural knowledge and practices (Civil, 2007) Recognize students’ cultural and linguistic resources (Gay, 2002; Ladson-Billings, 1995) Have robust knowledge of students, validate shared ideas and experiences, and connect instruction to students’ experiences and interests (Aguirre et al., 2013; Bartell, 2011; Hedges, Cullen, & Jordan, 2011; Wager, 2012) |
| 2. Establish classroom norms for participation | Recognize that student voice has implications for power and authority and builds agency (Cobb & Hodge, 2007; Turner, Dominguez, Maldonado, & Empson, 2013) Set up and guide discussions so that students from nondominant backgrounds develop strong mathematical identities (Hodge, 2006) Connect pedagogical practices to student participation (Boaler & Greeno, 2000; Wager, 2014) Question whose participation norms are valorized (Planas & Gorgorió, 2004) |
| 3. Position students as capable | Construct social structures that enable students to “develop strategies that help maintain certain positions and reduce others” (Planas & Civil, 2010, p. 145) Challenge and counteract societal stereotypes and inequities to which students and communities are subjected (Bartell, 2011; Gay, 2002; Ladson-Billings, 1995) Attend to how the curriculum may influence perceptions of students (Atweh, Bleicher, & Cooper, 1998) Share power in the classroom by allowing students to provide meaningful input in making decisions about classroom practices, curriculum, and assessment (Cornelius & Herrenkohl, 2004; Sheets, 2005) |
| 4. Monitor how students position each other | Assign competence to support students’ repositioning of one another (Cohen, Lotan, Scarloss, & Arellano, 1999; Featherstone et al., 2011) Attend to reification of existing status structures so as to reposition some students with their peers (Forman & Ansell, 2002) Position students to use one another as mathematical resources (Dunleavy, 2015) |
| 5. Attend explicitly to race and culture | Make connections to students’ mathematical, racial, and cultural identities (Battey, 2013; Martin, 2007) Recognize that certain groups have been positioned as anti-intellectual (Martin, 2009; Steele, 2003) |
Table 1 (continued) Equitable Mathematics Teaching Practices| Equitable practice | Examples of the practice |
| 6. Recognize multiple forms of discourse and language as a resource | Facilitate respect among students by cultivating culturally responsive relationships among students and validating possible differences in their language practices (Moschkovich, 2013) Coconstruct resources with students in moment-to-moment interactions around mathematics (Dominguez, 2014) Consider linguistic choices and acknowledge home language as a valid language of mathematics (Meaney, 2005; Setati, 2005) Bridge language practices through affirming students’ home languages, modeling code switching, and fostering interactional patterns familiar to students (Brenner, 1998; Howard, 2001; Lee, 1995) |
| 7. Press for academic success | Assess student learning, build on student strengths, explicitly communicate expectations for students, and communicate the teachers’ responsibility in student success (Morrison, Robbins, & Rose, 2008) Have high academic expectations while maintaining students’ cultural and psychological well-being rather than accept deficit views about students’ intellectual potential (Fine, 1986; Fordham, 1988) |
| 8. Attend to students’ mathematical thinking | Recognize, understand, and build from children’s understanding of mathematics (Carpenter, Fennema, Franke, Levi, & Empson, 1999) Respond to developmental needs so as not to expect a student to do mathematics they are not developmentally ready for (Jackson, 2009) |
| 9. Support development of a sociopolitical disposition | Incorporate critical texts, discuss controversial topics, serve the community, and allow social issues to drive instruction (Hickling-Hudson & Ahlquist, 2003; Hyland, 2005; Tate, 1995) Provide opportunities to explore sociopolitical topics using mathematics (Frankenstein, 2012; Gates & Jorgensen, 2009) Engage students in conversation about real-world problems and how mathematics can be used to examine them (Gutstein, 2006; Skovsmose, 1994) |
Drawing on Students’ Funds of Knowledge as They Make Sense of Problems and Persevere in Solving Them
Consider the cell (A in Figure 1) marking the intersection between Equitable Mathematics Teaching Practice 1 (draw on students’ funds of knowledge) and SMP1 (make sense of problems and persevere in solving them). To support students’ development of this SMP that includes students’ making sense of problems by “explaining to themselves the meaning of a problem and looking for entry points to its solution” as well as in “analyz[ing] givens, constraints, relationships, and goals” and in “continually ask[ing] themselves ‘Does this make sense?’” (NGA & CCSSO, 2010, p. 6), teachers could explicitly construct problems (or adapt problem contexts) connected to students’ experiences or community or family practices. For example, Turner et al. (2014) described lessons prospective teachers created that elicited and connected to students’ cultural funds of knowledge across multiple components of a mathematics lesson. In one lesson, prospective teachers designed a series of mathematics tasks about different ways to spend 25 tickets at a carnival on rides or food. Choosing how to use tickets at a local carnival was known to be an experience most of the students had engaged in, and the task was designed to support students in understanding that a number can be composed of a variety of addends. In this example, students made sense of the situation by considering things like their favorite rides and the fact that they did not have enough tickets to go on every ride and to eat all their favorite foods. Each student came up with different combinations of rides and food that met their own interests to try to maximize use of all tickets. The prospective teachers noted that students engaged in the task in multiple ways (finding different entry points) and showed increased engagement in comparison to tasks they had used previously. Research demonstrates that students benefit from instruction that draws upon their cultural and community-based knowledge (González, Moll, & Amanti, 2005; Ladson-Billings, 1995). Moreover, students are more likely to persevere in a problem that is of interest to them (Renninger, Ewen, & Lasher, 2002) and to make sense of a problem and identify an entry point if a task is introduced in a way that includes discussion of key contextual features (Jackson, Garrison, Wilson, Gibbons, & Shahan, 2013).
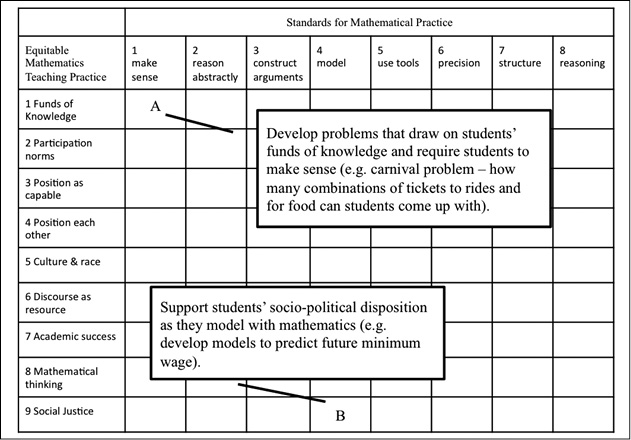
Figure 1. Framework for the intersection of equitable mathematics teaching practices and the SMP.
Supporting Students’ Sociopolitical Disposition as They Model With Mathematics
Consider the cell (B in Figure 1) marking the intersection between Equitable Mathematics Teaching Practice 9 (social justice) and SMP4 (model with mathematics). At this intersection, students would work on ill-defined problems from real-world contexts that require them to struggle to use mathematics to understand the problem (Koestler et al., 2013) in order to understand and change their world (Gutstein, 2006). For example, Powell (2012) described a unit she developed in which her students modeled with mathematics to predict the future minimum wage based on a given data set. In this unit, students were able to build on their own understanding and experience with various functions (quadratic, linear, piece-wise) to model real-world, relevant data to make predictions that would have an impact on their lives. This activity led to important discussions about decisions students made in choosing the subset of data and function that they used as well as the implications of a minimum versus living wage. Although the idea of supporting students to model with mathematics using a social justice context is gaining traction as a way to support students’ engagement in both practices (Cirillo, Bartell, & Wager, 2016; Felton, Anhalt, & Cortez, 2015), we recognize that this work is not without tensions. As both Bartell (2013) and Enyedy and Mukhopadhyay (2007) have found, teachers who bring in emotionally charged topics must be prepared to facilitate and respond to students’ struggles with the subject.
Call for Future Research
As articulated in the introduction, our call for research is based on our concerns that enacting the CCSSM without explicit attention to equity will only serve to reify existing inequities. We have three questions to pose to the mathematics education community that will support connections of equitable mathematics teaching practices to the SMP:
1. How can we theorize equitable mathematics teaching practices that support student engagement in the SMP?
2. In what ways are the teaching practices that attempt to align with the CCSSM supporting equitable learning opportunities?
3. What kinds of studies might support teachers to engage in equitable mathematics teaching practices that connect to the SMP?
For the first question, our framework offers a starting point with references in Table 1 to several scholars in the field who have been studying equitable mathematics teaching practices. Beyond a review of the literature, we see a need for the field to theorize how these studies of equity mathematics research are interwoven and can be connected specifically to the SMP. In our first example above, teachers who draw on students’ funds of knowledge may be supporting the development of making sense of problems (SMP1) while also supporting students in making connections between problems in school mathematics and their everyday experiences. In what other ways does this equitable mathematics teaching practice support students to develop other SMP?
With respect to the second question, several scholars are already studying the impact of the CCSSM on student learning, although few of these studies are connected to the ideas of opportunity to learn (see Esmonde, 2009, for an exception) and access. In a search using the terms common core, mathematics, and learning, we found 69 relevant peer-reviewed articles available through ERIC’s database. A large number (39%) of these articles appeared in NCTM’s three practitioner journals, and claims in over half of the articles (52%) are grounded in theory or analyses of curricula or tasks rather than in empirical findings. Only 25% of the articles explicitly addressed the impact of the CCSSM on opportunities for all students to learn. In particular, authors focused on students who qualify for special education services (learning disabilities, emotional behavioral disabilities, etc.; 13% of total articles), English language learners (6% of total articles), and students from low socioeconomic status backgrounds (4% of total articles). With few exceptions, we found that learning as measured by many of those studies does not necessarily consider the opportunities for all students to learn. As such, we suggest that the field needs to study classrooms to identify those teachers using the CCSSM and also enacting equitable mathematics teaching practices. These studies will shed light on how equitable practices are improving students’ opportunities to learn.
For the third question, we suggest that scholars whose research is centered in the SMP need to extend that work to also consider whether equity is attained in those classrooms. We also suggest that scholars whose research is centered in equitable mathematics teaching practices need to extend that work to also consider how those practices support students in their engagement with the SMP. Much as Koestler, Felton, Bieda, and Otten (2013) drew connections between the SMP and the NCTM process standards, we envision that for each of the SMP, there are activities/problems/practices that connect to each of the equitable mathematics teaching practices (i.e., examples that would populate each cell in the table). Our goal is to suggest to the field that this framework can be used for future research by studying the connections in each of the cells, columns, or rows. This framework would provide an opportunity for scholars across the mathematics education field to engage with the ideas of equitable mathematics teaching practices that support students to engage in the SMP no matter where they position their research. For example, scholars who study mathematical modeling might design a study around an individual cell in the table, such as the intersection of modeling and social justice as discussed above, or they might explore how each equitable mathematics teaching practice might be evidenced in their study of mathematical modeling. We also believe this framework provides an excellent opportunity for scholars across areas of mathematics education to collaborate on studies at the intersections of equitable mathematics teaching practices and the SMP.
Conclusion
In this commentary, we are (a) calling for research that attends to a critical topic connecting policy, research, and practice; (b) providing explicit questions we believe the field needs to address; and (c) offering a starting point (our framework) to identify studies that align with a wide range of research agendas while still addressing a central theme. By attending to these ideas, it is our hope that the field, as a community, can connect existing (and new) research to policy in order to support equitable practices that provide all students with the opportunity to learn mathematics. Without this, we see the CCSSM as yet another reform idea that, in the end, reproduces past inequities.
References
Aguirre, J. M., Turner, E. E., Bartell, T. G., Kalinec-Craig, C., Foote, M. Q., Roth McDuffie, A., & Drake, C. (2013). Making connections in practice: How prospective elementary teachers connect to children’s mathematical thinking and community funds of knowledge in mathematics instruction. Journal of Teacher Education, 64(2), 178–192. doi:10.1177/0022487112466900
Allensworth, E., Nomi, T., Montgomery, N., & Lee, V. E. (2009). College preparatory curriculum for all: Academic consequences of requiring algebra and English I for ninth graders in Chicago. Educational Evaluation and Policy Analysis, 31(4), 367–391. doi:10.3102/0162373709343471
Apple, M. W. (1992). Do the standards go far enough? Power, policy, and practice in mathematics education. Journal for Research in Mathematics Education, 23(5), 412–431. doi:10.2307/749562
Apple, M. W. (1999). The absent presence of race in educational reform. Race Ethnicity and Education, 2(1), 9–16. doi:10.1080/1361332990020102
Apple, M. W. (2000). Mathematics reform through conservative modernization? Standards, markets, and inequality in education. In J. Boaler (Ed.), Multiple perspectives on mathematics teaching and learning (pp. 243–259). Westport, CT: Ablex.
Atweh, B., Bleicher, R. E., & Cooper, T. J. (1998). The construction of the social context of mathematics classrooms: A sociolinguistic analysis. Journal for Research in Mathematics Education, 29(1), 63–82. doi:10.2307/749718
Atweh, B., Calabrese-Barton, A., Borba, M. C., Gough, N., Keitel, C., Vistro-Yu, C., & Vithal, R. (Eds.). (2008). Internationalisation and globalization in mathematics and science education. Dordrecht, the Netherlands: Springer.
Atweh, B., & Clarkson, P. (2001). Internationalisation and globalisation of mathematics education: Towards an agenda for research/action. In B. Atweh, H. Forgasz, & B. Nebres (Eds.), Sociocultural research on mathematics education: An international perspective (pp. 77–94). Mahwah, NJ: Erlbaum.
Bartell, T. G. (2011). Caring, race, culture, and power: A research synthesis toward supporting mathematics teachers in caring with awareness. Journal of Urban Mathematics Education, 4(1), 50–74.
Bartell, T. G. (2013). Learning to teach mathematics for social justice: Negotiating social justice and mathematical goals. Journal for Research in Mathematics Education, 44(1), 129–163. doi:10.5951/jresematheduc.44.1.0129
Battey, D. (2013). “Good” mathematics teaching for students of color and those in poverty: The importance of relational interactions within instruction. Educational Studies in Mathematics, 82(1), 125–144. doi:10.1007/s10649-012-9412-z
Bidwell, A. (2014, August 20). Common Core support in free fall. U.S. News & World Report. Retrieved from http://www.usnews.com/news/articles/2014/08/20/common-core-support-waning-most-now-oppose-standards-national-surveys-show
Boaler, J., & Greeno, J. G. (2000). Identity, agency, and knowing in mathematical worlds. In J. Boaler (Ed.), Multiple perspectives on mathematics teaching and learning (pp. 171–200). Westport, CT: Ablex.
Brenner, M. E. (1998). Adding cognition to the formula for culturally relevant instruction in mathematics. Anthropology & Education Quarterly, 29(2), 214–244. doi:10.1525/aeq.1998.29.2.214
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Cirillo, M., Bartell, T. G., & Wager, A. A. (2016). Teaching mathematics for social justice through mathematical modeling. In C. R. Hirsch & A. Roth McDuffie (Eds.), Annual perspective in mathematics education 2016: Mathematical modeling and modeling mathematics (pp. 87–96). Reston, VA: NCTM.
Civil, M. (2007). Building on community knowledge: An avenue to equity in mathematics education. In N. S. Nassir & P. Cobb (Eds.), Improving access to mathematics: Diversity and equity in the classroom (pp. 105–117). New York, NY: Teachers College Press.
Cobb, P., & Hodge, L. (2007). Culture, identity, and equity in mathematics classrooms. In N. S. Nasir & P. Cobb (Eds.), Improving access in mathematics: Diversity and equity in the classroom (pp. 159–172). New York, NY: Teachers College Press.
Cohen, E. G., Lotan, R. A., Scarloss, B. A., & Arellano, A. R. (1999). Complex instruction: Equity in cooperative learning classrooms. Theory into Practice, 38(2), 80–86. doi:10.1080/00405849909543836
Cornelius, L. L., & Herrenkohl, L. R. (2004). Power in the classroom: How the classroom environment shapes students’ relationships with each other and with concepts. Cognition and Instruction, 22(4), 467–498. doi:10.1207/s1532690Xci2204_4
Cuban, L. (1990). Reforming again, again, and again. Educational Researcher, 19(1), 3–13. doi:10.3102/0013189X019001003
Diversity in Mathematics Education (DiME) Center for Learning and Teaching. (2007). Culture, race, power, and mathematics education. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 405–434). Charlotte, NC: Information Age.
Dominguez, H. (2014). Reconocer: Recognizing resources with English learners in mathematics. In T. G. Bartell & A. Flores (Eds.), TODOS research monograph 3: Embracing resources of children, families, communities, and cultures in mathematics learning (pp. 138–168). Tempe, AZ: TODOS: Mathematics for All.
Dunleavy, T. K. (2015). Delegating mathematical authority as a means to strive toward equity. Journal of Urban Mathematics Education, 8(1), 62–82.
Enyedy, N., & Mukhopadhyay, S. (2007). They don’t show nothing I didn’t know: Emergent tensions between culturally relevant pedagogy and mathematics pedagogy. Journal of the Learning Sciences, 16(2), 139–174. doi:10.1080/10508400701193671
Eppley, K. (2015). Seven traps of the Common Core State Standards. Journal of Adolescent & Adult Literacy. Advance online publication. doi:10.1002/jaal.431
Ernest, P. (2009). Mathematics education ideologies and globalization. In P. Ernest, B. Greer, & B. Sriraman (Eds.), Critical issues in mathematics education (pp. 67–110). Charlotte, NC: Information Age.
Esmonde, I. (2009). Ideas and identities: Supporting equity in cooperative mathematics learning. Review of Educational Research, 79(2), 1008–1043. doi:10.3102/0034654309332562
Featherstone, H., Crespo, S., Jilk, L. M., Oslund, J. A., Parks, A. N., & Wood, M. B. (2011). Smarter together! Collaboration and equity in the elementary math classroom. Reston, VA: NCTM.
Felton, M. D., Anhalt, C. O., & Cortez, R. (2015). Going with the flow: Challenging students to make assumptions. Mathematics Teaching in the Middle School, 20(6), 342–349. doi:10.5951/mathteacmiddscho.20.6.0342
Fine, M. (1986). Why urban adolescents drop into and out of public high school. Teachers College Record, 87(3), 393–409.
Fordham, S. (1988). Racelessness as a factor in Black students’ school success: Pragmatic strategy or pyrrhic victory? Harvard Educational Review, 58(1), 54–85. doi:10.17763/haer.58.1.c5r77323145r7831
Forman, E. A., & Ansell, E. (2002). Orchestrating the multiple voices and inscriptions of a mathematics classroom. Journal of the Learning Sciences, 11(2–3), 251–274. doi:10.1080/10508406.2002.9672139
Frankenstein, M. (2012). Beyond math content and process: Proposals for underlying aspects of social justice education. In A. A. Wager & D. W. Stinson (Eds.), Teaching mathematics for social justice: Conversations with educators (pp. 49–62). Reston, VA: NCTM.
Gates, P., & Jorgensen, R. (2009). Foregrounding social justice in mathematics teacher education. Journal of Mathematics Teacher Education, 12(3), 161–170. doi:10.1007/s10857-009-9105-4
Gates, P., & Vistro-Yu, C. (2003). Is mathematics for all? In A. J. Bishop, M. A. Clements, C. Keitel, J. Kilpatrick, & F. K. S. Leung (Eds.), Second international handbook of mathematics education (pp. 31–73). Dordrecht, The Netherlands: Kluwer Academic Publishers. doi:10.1007/978-94-010-0273-8_3
Gay, G. (2002). Preparing for culturally responsive teaching. Journal of Teacher Education, 53(2), 106–116. doi:10.1177/0022487102053002003
González, N., Moll, L. C., & Amanti, C. (2005). Funds of knowledge: Theorizing practices in households, communities, and classrooms. Mahwah, NJ: Lawrence Erlbaum Associates.
Gutstein, E. (2006). Reading and writing the world with mathematics: Toward a pedagogy for social justice. New York, NY: Routledge.
Gutstein, E. (2008). The political context of the National Mathematics Advisory Panel. The Montana Mathematics Enthusiast, 5, 415–422. http://www.math.umt.edu/tmme/vol5no2and3/TMME_vol5nos2and3_a21_pp.415_422.pdf
Gutstein, E. (2009). The politics of mathematics education in the US: Dominant and counter agendas. In B. Greer, S. Mukhopadhyay, A. B. Powell, & S. Nelson-Barber (Eds.), Culturally responsive mathematics education (pp. 137–164). New York, NY: Routledge.
Gutstein, E. (2010). The Common Core State Standards initiative: A critical response. Journal of Urban Mathematics Education, 3(1), 9–18.
Hand, V. (2012). Seeing culture and power in mathematical learning: Toward a model of equitable instruction. Educational Studies in Mathematics, 80(1–2), 233–247. doi:10.1007/s10649-012-9387-9
Hedges, H., Cullen, J., & Jordan, B. (2011). Early years curriculum: Funds of knowledge as a conceptual framework for children’s interests. Journal of Curriculum Studies, 43(2), 185–205. doi:10.1080/00220272.2010.511275
Herbel-Eisenmann, B., Bartell, T. G., Breyfogle, M. L., Bieda, K., Crespo, S., Dominguez, H., & Drake, C. (2013). Strong is the silence: Challenging interlocking systems of privilege and oppression in mathematics teacher education. Journal of Urban Mathematics Education, 6(1), 6–18.
Hickling-Hudson, A. R., & Ahlquist, R. (2003). Whose culture? The colonising school and the miseducation of indigenous children: Implications for schooling in Australia. Journal of Postcolonial Education, 2(2), 15–35.
Hodge, L. L. (2006). An orientation on the mathematics classroom that emphasizes power and identity: Reflecting on equity research. The Urban Review, 38(5), 373–385. doi:10.1007/s11256-006-0041-7
Howard, T. C. (2001). Telling their side of the story: African-American students’ perceptions of culturally relevant teaching. The Urban Review, 33(2), 131–149. doi:10.1023/A:1010393224120
Hyland, N. E. (2005). Being a good teacher of Black students? White teachers and unintentional racism. Curriculum Inquiry, 35(4), 429–459. doi:10.1111/j.1467-873X.2005.00336.x
Jackson, K. (2009). The social construction of youth and mathematics: The case of a fifth-grade classroom. In D. B. Martin (Ed.), Mathematics teaching, learning, and liberation in the lives of black children (pp. 175–199). New York, NY: Routledge.
Jackson, K., Garrison, A., Wilson, J., Gibbons, L., & Shahan, E. (2013). Exploring relationships between setting up complex tasks and opportunities to learn in concluding whole-class discussions in middle-grades mathematics instruction. Journal for Research in Mathematics Education, 44(4), 646–682. doi:10.5951/jresematheduc.44.4.0646
Kilpatrick, J. (2007). A commentary on research commentaries. Journal for Research in Mathematics Education, 38(2), 106–107.
Koestler, C., Felton, M. D., Bieda, K. N., & Otten, S. (2013). Connecting the NCTM Process Standards and the CCSSM practices. Reston, VA: NCTM.
Ladson-Billings, G. (1995). Toward a theory of culturally relevant pedagogy. American Educational Research Journal, 32(3), 465–491. doi:10.3102/00028312032003465
Lee, C. D. (1995). A culturally based cognitive apprenticeship: Teaching African American high school students skills in literary interpretation. Reading Research Quarterly, 30(4), 608–630. doi:10.2307/748192
Lipman, P. (2012). Neoliberal urbanism, race, and equity in mathematics education. Journal of Urban Mathematics Education, 5(2), 6–17.
Martin, D. B. (2007). Beyond missionaries or cannibals: Who should teach mathematics to African American children? The High School Journal, 91(1), 6–28. doi:10.1353/hsj.2007.0023
Martin, D. B. (2008). E(race)ing race from a national conversation on mathematics teaching and learning: The National Mathematics Advisory Panel as white institutional space. The Montana Mathematics Enthusiast, 5(2&3), 387–398.
Martin, D. B. (2009). Researching race in mathematics education. Teachers College Record, 111(2), 295–338.
Martin, D. B. (2013). Race, racial projects, and mathematics education. Journal for Research in Mathematics Education, 44(1), 316–333. doi:10.5951/jresematheduc.44.1.0316
Meaney, T. (2005). Mathematics as text. In A. Chronaki & I. M. Christiansen (Eds.), Challenging perspectives on mathematics classroom communication (pp. 109–141). Greenwich, CT: Information Age.
Morrison, K. A., Robbins, H. H., & Rose, D. G. (2008). Operationalizing culturally relevant pedagogy: A synthesis of classroom-based research. Equity & Excellence in Education, 41(4), 433–452. doi:10.1080/10665680802400006
Moschkovich, J. (2013). Principles and guidelines for equitable mathematics teaching practices and materials for English language learners. Journal of Urban Mathematics Education, 6(1), 45–57.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Author. Retrieved from http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf
Philipp, R. A. (2007). Mathematics teachers’ beliefs and affect. In F. K. Lester, Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 257–318). Charlotte, NC: Information Age.
Planas, N., & Civil, M. (2010). Discourse processes in critical mathematics education. In H. Alrø, O. Ravn, & P. Valero (Eds.), Critical mathematics education: Past, present and future (pp. 145–159). Rotterdam, The Netherlands: Sense Publishers.
Planas, N., & Gorgorió, N. (2004). Are different students expected to learn norms differently in the mathematics classroom? Mathematics Education Research Journal, 16(1), 19–40. doi:10.1007/BF03217389
Powell, G. C. (2012). Teaching mathematics for social justice: The end of “when are we ever going to use this?” In A. A. Wager & D. W. Stinson (Eds.), Teaching mathematics for social justice: Conversations with educators (pp. 187–197). Reston, VA: NCTM.
Renninger, K. A., Ewen, L., & Lasher, A. K. (2002). Individual interest as context in expository text and mathematical word problems. Learning and Instruction, 12(4), 467–490. doi:10.1016/S0959-4752(01)00012-3
Setati, M. (2005). Teaching mathematics in a primary multilingual classroom. Journal for Research in Mathematics Education, 36(5), 447–466. doi:10.2307/30034945
Sheets, R. H. (2005). Diversity pedagogy: Examining the role of culture in the teaching-learning process. Boston, MA: Allyn & Bacon.
Skovsmose, O. (1994). Towards a critical mathematics education. Educational Studies in Mathematics, 27(1), 35–57. doi:10.1007/BF01284527
Skovsmose, O., & Valero, P. (2002). Democratic access to powerful mathematical ideas. In L. D. English (Ed.), Handbook of international research in mathematics education (pp. 383–407). Mahwah, NJ: Lawrence Erlbaum Associates.
Steele, C. (2003). Stereotype threat and African-American student achievement. In T. Perry, C. Steele, & A. Hilliard III (Eds.), Young, gifted, and black: Promoting high achievement among African American students (pp. 109–130). Boston, MA: Beacon Press.
Tate, W. F. (1995). Returning to the root: A culturally relevant approach to mathematics pedagogy. Theory Into Practice, 34(3), 166–173. doi:10.1080/00405849509543676
Turner, E., Aguirre, J., Bartell, T., Drake, C., Foote, M., & Roth McDuffie, A. (2014). Making meaningful connections with mathematics and the community: Lessons from prospective teachers. In T. G. Bartell & A. Flores (Eds.), TODOS research monograph 3: Embracing resources of children, families, communities, and cultures in mathematics learning (pp. 60–100). Tempe, AZ: TODOS: Mathematics for All.
Turner, E., Dominguez, H., Maldonado, L., & Empson, S. (2013). English learners’ participation in mathematical discussion: Shifting positioning and dynamic identities. Journal for Research in Mathematics Education, 44(1), 199–234. doi:10.5951/jresematheduc.44.1.0199
Ujifusa, A. (2015, June 30). A ‘common-core math’ problem: How many states have adopted the standards? Education Week. Retrieved from http://blogs.edweek.org/edweek/state_edwatch/2015/06/a_common_core_math_problem_how_many_states_have_adopted_the_standards.html
Wager, A. A. (2012). Incorporating out-of-school mathematics: From cultural context to embedded practice. Journal of Mathematics Teacher Education, 15(1), 9–23. doi:10.1007/s10857-011-9199-3
Wager, A. A. (2014). Noticing children’s participation: Insights into teacher positionality toward equitable mathematics pedagogy. Journal for Research in Mathematics Education, 45(3), 312–350. doi:10.5951/jresematheduc.45.3.0312
Woodrow, D. (2003). Mathematics, mathematics education and economic conditions. In A. Bishop, M. A. Clements, C. Keitel-Kreidt, J. Kilpatrick, & F. K. S. Leung (Eds.), Second international handbook of mathematics education. Retrieved from http://www.esri.mmu.ac.uk/respapers/papers-pdf/Paper%20-%20maths,%20maths%20ed%20&%20economics.pdf. doi:10.1007/978-94-010-0273-8_2
Authors
Tonya Bartell, Department of Teacher Education, Michigan State University, 620 Farm Lane, East Lansing, MI 48824; [email protected]
Anita Wager, University of Wisconsin-Madison, 225 N. Mills Street, Madison, WI 53706; [email protected]
Ann Edwards, Carnegie Foundation for the Advancement of Teaching, 51 Vista Lane, Stanford, CA 94305; [email protected]
Dan Battey, Graduate School of Education, Rutgers University, 10 Seminary Place, 229C, New Brunswick, NJ 08901; [email protected]
Mary Foote, Queens College, Powdermaker Hall, Room 054W, Queens, NY 11367; [email protected]
Joi Spencer, Department of Learning and Teaching, University of San Diego, 5998 Alcala Park, Mother Rosalie Hill Hall, San Diego, CA 92108; [email protected]
Submitted November 7, 2014
Accepted July 24, 2015