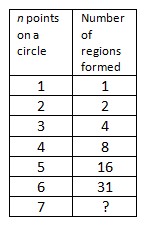
Going Around in Circles 
If we pick any two distinct points on a circle, and connect them with a chord, the chord will divide the interior of the circle into two distinct, nonintersecting regions. If we pick three distinct points on a circle and connect each pair of them with a chord, we can form four distinct, nonintersecting regions.

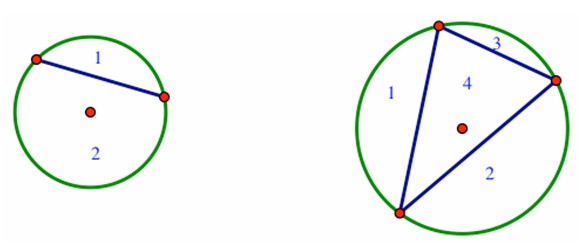
What is the maximum number of nonintersecting regions that we can form by selecting four distinct points on a circle and connecting each pair of them with a chord? By selecting five distinct points? Six distinct points? And of course, then, ndistinct points?

Some Ponderings:  

Recall that November’s Problem to Ponder was as follows:

If we pick any two distinct points on a circle and connect them with a chord, the chord will divide the interior of the circle into two distinct, nonintersecting regions. If we pick three distinct points on a circle and connect each pair of them with a chord, we can form four distinct, nonintersecting regions. 

What is the maximum number of nonintersecting regions that we can form from the chords connecting four distinct points on a circle? Five distinct points? Six distinct points? ndistinct points?

This problem starts out innocently enough. We can see above that 2 regions are formed by 1 chord connecting 2 points on a circle and that 4 regions are formed by chords connecting 3 points on a circle.  Then we might notice that 8 regions can be formed by chords connecting 4 points on a circle and 16 regions can be formed by chords connecting 5 points on a circle—ah, life looks good here! A nice 2^n-1 pattern, we say, where n is the number of points on the circle!

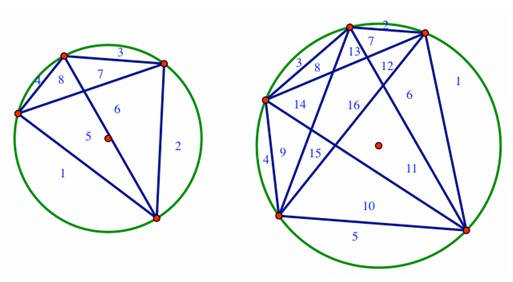
And then our hopes are quickly dashed when we look at the case of 6 points. 

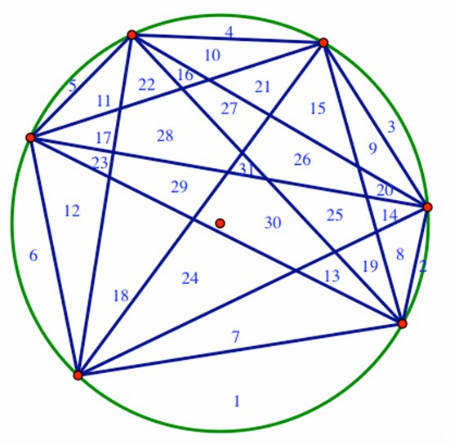
The powers of 2 pattern breaks down when we choose 6 points on a circle. The maximum number of regions that we can obtain from crossing chords with 6 points is 31. Students quickly realize that if 3 or more chords cross at the same point in the interior of a circle, then they don’t obtain the maximum possible number of regions. For example, the vertices of a regular hexagon on a circle will generate only 30 distinct regions from its crossed chords. To obtain the maximum number of regions, students must permit at most 2 chords to intersect at the same point.

This, then, is your mathematical holiday present—ponder away some more on this one!

More Ponderings: 

Recall that November’s Problem to Ponder was as follows:

If we pick any two distinct points on a circle and connect them with a chord, the chord will divide the interior of the circle into two distinct nonintersecting regions. If we pick three distinct points on a circle and connect each pair of them with a chord, we will form four distinct, nonintersecting regions. 

What is the maximum number of nonintersecting regions that we can form from the chords connecting four distinct points on a circle? Five distinct points? Six distinct points? ndistinct points?

In last month’s ponderings, we discovered that a seductive doubling pattern for this problem vanishes at n = 6 points. We found that 8 regions are formed by chords joining 4 points, and 16 regions are formed by chords joining 5 points, but then 31 regions are formed by chords joining 6 points!

How many regions can be formed by the chords joining 7 points on a circle?

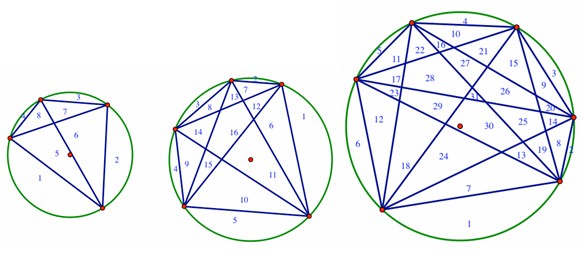
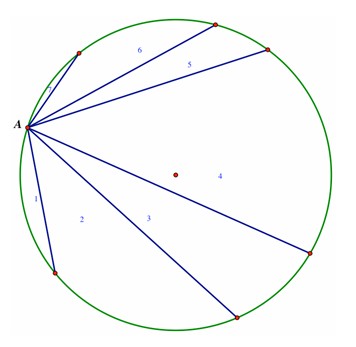
There are various ways to look for patterns or to count regions when additional points on the circle are chosen. Let’s consider one approach that I have seen students take.

In the succession of diagrams shown below for seven points, we notice that a new subregion is formed in the circle each time a chord meets a vertex and each time a chord crosses another chord. First, 7 regions are formed by constructing all the chords with point A as a vertex. 

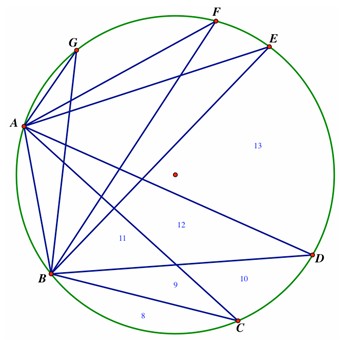
Next, an additional (1 + 2 + 3 + 4 + 5), or 15, regions are formed by constructing all the new chords from point B (see below). Segment BC forms region 8, segment BD forms regions 9 and 10, segment BE forms regions 11, 12, and 13, and so on. Each time a chord crosses a previously constructed chord, it adds another region, as also happens each time a chord meets a vertex, since previous regions are split into two pieces each time a chord crosses either another chord or meets a vertex. 

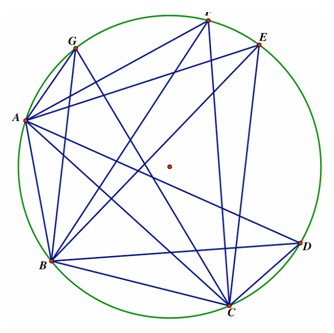
When we add the new chords from vertex C, CD forms 1 new region,CE forms 3 new regions, CF forms 5 new regions, and CG forms 7 new regions, because these chords cross 0, 2, 4, and 6 previous chords, respectively. Thus, we form an additional 1 + 3 + 5 + 7, or 16, new regions. 

The pattern for additional regions formed by chords from vertex D is as follows:  DEforms 1, DF forms 4, and DG forms 7 new regions, giving us 1 + 4 + 7, or 12, new regions. 

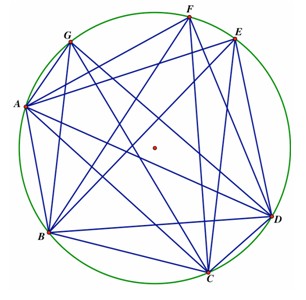
For chords from vertex E,EF forms 1 new region and EG forms 5 new regions, since it will cross 4 chords and then meet the vertex at G, yielding 1 + 5, or 6, new regions.

And finally, chord FGforms 1 additional region.  So, altogether we have 7 + (1+2+3+4+5) + (1+3+5+7) + (1+4+7) + (1+5) + 1, or 57, regions formed by the chords connecting 7 points. Our pattern is distinctly nonlinear, isn’t it! Lovely! 

Given the types of patterns that we see above, we might guess that choosing 8 points on a circle and connecting them by chords will form 8 + (1+2+3+4+5+6) + (1+3+5+7+9) + (1+4+7+10) + (1+5+9) + (1+6) + 1, or 99, regions.

If we look back at an earlier Problem to Ponder, “Figuring out Figurate Numbers” (September, 2011), we might notice that the pattern above is also a sum of figurate numbers. For example, the number of regions formed by chords joining 8 points on the circle is as follows: 

     8  (the number of points)

+ 21 (the 6th triangular number)

+ 25 (the 5th square number)

+ 22 (the 4th pentagonal number)

+ 15 (the 3rd hexagonal number)

+  7  (the 2nd heptagonal number)

 + 1  (the 1st octagonal number)

Your students may find all sorts of other ways to identify patterns in this problem. The next question is, Can we find a closed form formula that will give us the number of regions formed by chords connecting n points? That is, can we express the number of regions in a circle as a function of n, the number of points on it connected by chords?

If the function happens to be a polynomial function of n, then the method of finite differences on the sequence of successive terms can tip us off about what the degree of that polynomial will be. If successive differences between the terms of a sequence eventually result in a constant sequence, then the function that generates the original sequence of terms will be a polynomial, and the degree of the polynomial will be the same as the number of difference sequences that it takes to yield that constant difference. Consider the table below:

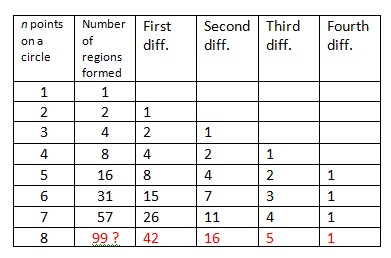
The fourth successive difference column is a constant in our problem. So the function that yields the number of regions formed by n points on a circle will be a polynomial of degree 4. Notice that the difference between two successive terms is similar to a difference quotient in calculus, and recall that if a polynomial function is of degree p, its pth derivative is a constant function. Similarly, if the pth finite difference is a constant, the original sequence is generated by a polynomial of degree p.

We’ll return with some more ponderings on Going Around in Circles next month. Meantime, see if you can find a way to determine that fourth-degree polynomial, with or without the method of finite differences.