This lesson is intended to be an introduction to various function
types, including linear, exponential, quadratic, and piecewise.
Therefore, use this activity to pique students’ interest in functions
and to allow them to deduce algebraic equations. However, as you work
through the lesson, do not expect exact answers. Rather, focus on
allowing students to develop an understanding of the multiple
representations of functions and concepts such as constant vs. variable
movement. Lesson 2 in this unit, How Did I Move?, works well when you
are introducing the slope-intercept form of linear equations.
 How Did I Move?
How Did I Move?
Note that
you may wish to repeat the corresponding parts of this lesson at that
time.
Preparation
The lesson is designed to allow students to investigate six graph
pairs over two days. Use Day 3 to reflect on the content of Days 1 and 2.
 How Should I Move? Graphs Activity Sheet
How Should I Move? Graphs Activity Sheet
Before Day 1, choose 6 graph pairs from the How Should I Move? Graphs Activity Sheet. Graph Pairs 1–6 deal with linear graphs, while Graph
Pairs 7–9 include exponential and quadratic graphs. The linear graphs
are generally easier for students to explore algebraically. If you wish
to include a discussion of constant vs. variable movement, then include
at least one of Graph Pairs 7–9.
 How Should I Move? Overhead
How Should I Move? Overhead
If only one motion detector is available, prepare the How Should I Move? Overhead by writing the 6 graph pair numbers in the 6 empty boxes. For
example, if you choose to use Graph Pairs 1–4, 7, and 8, the completed
table make look like this:
| Groups | Graph Pairs |
| Day 1 | Day 2 |
| Groups 1 & 2 | 1 | 4 |
| Groups 3 & 4 | 2 | 7 |
| Groups 5 & 6 | 3 | 8 |
Before class begins on Day 1, set up the motion detector to
collect data and project the results to the front of the classroom. Set
the motion detector to collect data in feet, to work best with the
activity sheets provided.
Introducing the Activity
Ask a student who arrives early to walk in
front of the motion detector so the resulting graph can be displayed.
Students’ interest will be piqued as they enter the classroom if they
see a student’s movements creating a graph. Allow a few minutes for
students to play with the motion detector and graphs before beginning
the formal lesson. Note that graphs begin at 2 feet from the motion
detector.
Explain to the class that over the next 2 days, they will be
trying to re-create graphs by moving in front of the motion detector.
They will work in groups, and groups will be paired so that they
compete with another group to create the best graph. Each group will be
given 2 chances to make the best graph. For example, group 1 tries to
create Graph A twice. Then, group 2 tries to create the same graph.
Group 2 will then begin first for Graph B. Refer to one of the graphs
they created when they first came in, or show the sample graph below:
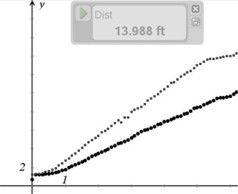
If only one motion detector is available:
Divide the class into 6 groups. Each group should have at least
3 students so that one student runs the motion detector, the second
student writes down the strategy, and the third student moves to create
the graph. If it is not practical in your class to have six groups,
separate the class into equal-sized groups so that all students will
have a chance to use the motion detector. Other students in the group
could be assigned the task of suggesting the movement if group size
exceeds 3.
Display the How Should I Move? Overhead with the appropriate graph pair numbers filled in. Ensure
students know their group assignments and the graph pairs they are to
create on the motion detector. All students in the class should
complete the How Should I Move? Questions Activity Sheet for each graph pair, using the graphs created by the
groups assigned to that graph pair. Once all students have an
opportunity to complete the activity sheet for a graph pair, the group
responsible for creating the graphs on the motion detector should share
their answers.
 How Should I Move? Questions Activity Sheet
How Should I Move? Questions Activity Sheet
If multiple motion detectors are available:
Separate the class into groups of 3. Let students know that
during each trial, one student runs the motion detector, the second
student writes down the strategy, and the third student moves to create
the graph. Pair groups together so they can compete to create the best
graph. Then, let the class know which graph pairs they will be
responsible for and distribute the motion detectors and graphing
calculators or computers to each pair of groups.
Main Activity (Days 1 and 2)
 How Should I Move? Graphs Activity Sheet
How Should I Move? Graphs Activity Sheet
 How Should I Move? Questions Activity Sheet
How Should I Move? Questions Activity Sheet
Distribute the How Should I Move? Graphs Activity Sheet to each group. Place a pile of the How Should I Move? Questions Activity Sheets in a convenient location; each student will need a copy for each of the graph pairs being
explored.
Have students follow the How Should I Move? Questions Activity Sheet in order. If only one motion detector is available, each
student should make 2 conjectures about the type of movement that may
be needed to create the graphs (Question 2) before the assigned groups
try to create the graphs on the motion detector. If multiple motion
detectors are available, groups may work at their own pace.
Now the competition will begin. The assigned groups should take
turns competing to create the best graphs. All students will sketch the
best graphs from the motion detector and record the group number for
the best walker. If the two groups are not successful, allow other
groups to try to create the graphs. Do not provide any hints.
After the groups have created the first pair of graphs, ask all
the groups to read their conjectures. Allow for a discussion, asking
the groups that participated in the trials to provide answers to
Questions 5–8. When answering Question 7, encourage students to discuss
their starting position, speed, and the times and locations where they
had to change their movements. For example, Graph Pair 1 has the same
starting location for both graphs, but a faster speed is required to
create Graph B.
 How Should I Move? Questions Answer Key
How Should I Move? Questions Answer Key
When 3 graph pairs have been completed, have students attempt Question 9. Refer to the How Should I Move? Questions Answer Key
as you circulate through the room and assist students. They may use
either the original graph or their sketch to complete the table.
Students will very likely struggle with the equation(s). It may help to
first write an explanation of the movements using numbers, and then go
back to try the equation(s). You may give students some guidance using
one of the graphs as an example, and have them attempt the others on
their own. Move around the room and ask students about the patterns
they see in their data.
Each group should present their answer to Question 9. Have
students list the equation(s) they came up with on the board, and
discuss how they are the same and different, how they relate to the
movements, and how they relate to the graphs of time vs. distance.
Day 2 should largely mimic Day 1 with students competing to
create the best graphs for 3 graph pairs. As students struggle with
more difficult graphs or graphs that are impossible to create using the
motion detector, encourage them to explore the activity without
providing hints. Again, do not expect exact equations. Tables,
equations, and explanations that approximate the given graphs are
sufficient to understand the relationships between the representations.
Analysis (Day 3)
Have students share the equations they've deduced over the past
two days. If students were unable to come up with any equations, begin
sharing with students algebraic representations of graphs. For example,
in Graph Pair 7, discuss the doubling and halving patterns. Ask how
doubling and halving might be represented symbolically, working up to
the representation 2x. Ask students to volunteer
their equations, or provide correct equations and have students verify
that they represent the graphs accurately. Do this until all 6 graph
pairs have been discussed.
 Comparing Graph Pairs Activity Sheet
Comparing Graph Pairs Activity Sheet
Have students complete the Comparing Graph Pairs Activity Sheet as a summary activity. Depending on which graph pairs
you chose to use for this activity, some questions may be left blank.
You may choose to review the answer key (provided with the activity
sheet) with the class, and share with students which questions cannot
be answered. Alternatively, you may let students consider all the
questions and decide for themselves which do not have answers. For
example, if you did not choose Graph Pairs 4 or 9, there will be no
answer to Question 3, but you may leave it to the students to discover
this. When everyone has completed this activity sheet, have students
share their answers with the class. Lead a discussion of the answers as
a closure activity for the lesson.
Questions for Students
1. How could you move to create the graph?
[Answers will vary, but students should discuss position, speed, and direction.]
2. How did you move differently to create this graph than you did to create the previous graph?
[Answers will vary, but students should again discuss changes in position, speed, and direction.]
3. How can you tell by looking at a graph whether you should move at a constant rate or a variable rate?
[Encourage students to make the connection from the graph
to the movement and from the movement back to the graph. After a few
graphs, students should begin to recognize that a line or line segment
is created using constant movement, and a curve is created using
variable movement.]
4. How do different function types lead to different graphs, tables, and equations?
[Answers will vary. This is a question students should revisit several times as they work through the activities.]
5. Which graphs were unique?
[Answers will vary, but encourage students to discuss
distinctive characteristics of graphs such as changes in movement
(e.g., moving for part of the graph and standing still for another
part).]
6. What other kinds of graphs do you think could be created using a motion detector?
[Only functions can be created on a motion detector. This is a great time to discuss how the vertical line test relates to this activity. A vertical line on the graph represents all
the distances at a given time. A graph fails the vertical line test if
more than one point of the graph goes through a vertical line. This
means a person would have to be at more than one distance from the
motion detector at a point in time.]
Teacher Reflection
- How did you ensure that students understood the relationships among the movement, graph, table, and algebraic equation?
- Were students actively engaged in this lesson?
- Did students meet the objectives of the lesson? If not, what should be done in subsequent lessons?
- Was students’ level of enthusiasm/involvement high or low? Explain why.
- How did students demonstrate understanding of the materials presented?
- What, if any, issues arose with classroom management? How did
you correct them? If you use this lesson in the future, what could you
do to prevent these problems?