45–60 minutes

Description

Measure circular objects to explore the relationship between circumference and diameter of a circle in order to discover the ratio, Pi.

Materials

• pieces of string, approximately 48" long, or flexible tape measures
• Flexible measuring tapes will be easier for some students to manipulate than string.
• circular objects to be measured
• On some objects, a point could be placed on the round objects that shows the center.
• Circumference Activity Sheet
• Circumference Activity Answer Key
• calculators
• rulers
• Circle Tool Interactive
• (optional) Sir Cumference and the First Round Table: A Math Adventure by Cindy Neuschwander (used in Extension)

Introduce

Have students work in partners or small groups. Students should measure the circumference and the diameter of the objects that they brought to school. Students will likely have little trouble measuring the diameter, although they may have some difficulty identifying the exact middle of an object. To measure the circumference, students will likely need some assistance. An effective method for measuring the circumference is to wrap a string around the object and then measure the string, or to use flexible measuring tapes. To ensure accuracy, care should be taken to keep the string taut when measuring the circular object.
Students should be allowed to select which unit of measurement to use. However, instruct students to use the same unit for the circumference and the diameter.

Teacher Note:

Be prepared with additional items of varying sizes. Items that are too small (such as a dime) and too large (such as the opening of an umbrella) tend to be less accurate.

Explore

Students should record the following information in the Circumference Activity Sheet (download from Materials section above).

• Description of each object
• Circumference of each object
• Diameter of each object
• Circumference divided by diameter

After the measurements have been recorded, a calculator can be used to divide the circumference by the diameter. Students should answer both questions on the bottom of worksheet. Encourage students to note any numbers in the last column that seem to be outliers, and have them check to see if their measurements for these rows are realistic.

Teacher Notes:

Strategies for organizing activity:

Have students bring in the circular objects the day before and place them in stations around the room, then have students rotate through.

Have a student model the procedure of measuring the diameter and circumference before all students engage in the activity.

Synthesize

When all groups have completed the measurements and calculations, conduct a whole-class discussion. Rather than having students present each individual object, record each group’s average on the board. Discuss the averages and note any interesting findings. Also be sure to discuss the relationship between a circle’s diameter and its radius. The diameter of a circle is 2 times the radius or the radius is half of the diameter. Additionally, since there is a relationship between radius and diameter, you can also use the formula C = 2πr, since the diameter is twice the radius.

Teacher Notes:

Why is it important to measure more than one circular object? (SMP 6)

Did the outlier come from a measurement or calculation error? (SMP 6) The teacher may wish to point out that when cullecting real-life data, not every outlier is a mistake.

Further discussion could include whether any groups obtained ratios that appeared to be outliers, and how they verified their results. You may wish to use the Circle Tool interactive as a demonstration tool. This applet allows students to see many other circles of various sizes, as well as the corresponding ratio of circumference to diameter.

Teacher Notes:

• What do you notice when we all divided the circumference of each circle by its diameter? (SMP 8)

Explain that each group has found an approximation for the ratio of the circumference to the diameter, and this ratio has a special name: π. If students measured in inches, you may find that their ratio is less accurate, possibly due to a higher potential of measurement error. Based on their findings and the activity so far, have students try and generate a rule for this unique ratio, pi.

Because of this relationship, algebraic notation can be used to write circumference ÷ diameter = π or, said another way, π = C/d which leads to the following formula for circumference: C = π × d.

Teacher Notes:

When would it be useful to know the circumference of a circle?

Point out that groups within the class may have obtained slightly different approximations for π. Explain that determining the exact value of π is very hard to calculate, so approximations are often used. Discuss various approximations of π that are acceptable in your school’s curriculum/state assessments.

Teacher Notes:

Does circumference seem to have any relationship to any other mathematical concept that you are familiar with? perimeter

Describe some situations in which knowing the circumference (and how to calculate it) would be useful. [Bike tires are often described by their diameter. For instance, a 26-inch tire is a tire such that the diameter is 26". Each time the tire makes one complete rotation, the bike moves forward a distance equal to the circumference of the tire. Therefore, it would be helpful to know how to calculate the circumference based on the diameter.]

Assessment

Activity 1:

Each group can be given an apple pie (or other acceptable substitute) and will find its circumference by measuring the diameter and using the formula.

Activity 2:

Students should practice using the formula C = π × d as independent work. Their work on such problems could be used for assessment.

Real World Problem: According to Guinness, the world’s largest rice cake measured 5.83 feet in diameter. What is the circumference of this rice cake?

Real World Problem: The tallest tree in the world is believed to be the Mendocino Tree, a redwood near Ukiah, California, that is 112 meters tall! Near the ground, the circumference of this tree is about 9.85 meters. The age of a redwood can be estimated by comparing its diameter to trees with similar diameters. What is the diameter of the Mendocino Tree?

Extension (optional)

Activity 1:

In this lesson, students use a numeric approach to see the relationship between circumference and diameter. That is, students compute the ratio of circumference to diameter and then take the average for several objects. For a visual approach, have students plot the diameter of those objects along the horizontal axis of a graph and plot the circumference along the vertical axis. As shown below, a line of best fit with slope of roughly 3.14, or π, will approximate the points in the resulting scatterplot.

---

---

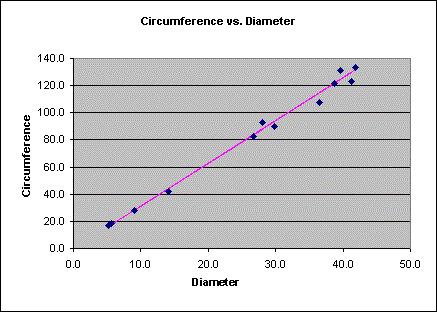
Activity 2:

Students can read and react to the book Sir Cumference and the First Round Table: A Math Adventure by Cindy Neuschwander. Within their groups, students can pose questions about the book and its mathematical accuracy, realism, and other components.

Activity 3:

In their groups, students can research the history of π and its calculation, approximation, and uses. In particular, they can research Archimedes’ method for estimating the area of a circle using inscribed polygons. The students could report their findings to the class.

Teacher Reflection

• How were students able to discover that the ratio of circumference to diameter is approximately π?
• Did students understand that the ratio of circumference to diameter (i.e., π) is an approximation? How were you able to help students understand why they had obtained different values for this approximation during the activity?
• What prior knowledge did students have of π (if any)? How did students’ prior knowledge affect the delivery of the lesson? What modifications did you need to make as a result, and how effective were these adjustments?
• How precise were student measurements? How did you assist students with their measurements?

Leave your thoughts in the comments below.