A Rematch for the Tortoise and the Hare!  
Some years after their famous race recounted in Aesop’s fable, the tortoise and the hare meet again and begin discussing their past run. The hare suggests that they conduct a game to simulate—or re-run—their storied race. He suggests the following rules: the tortoise will toss a coin, and if it comes up heads, he’ll move ahead 1 step, and if it comes up tails, he’ll move ahead 2 steps. The hare, being much faster, will toss a six-sided number cube, and he’ll move the number of steps shown on top of the cube, from 1 to 6. The tortoise replies that these rules will be acceptable, but only if the contestants agree that the winner must land on the last space of the racetrack by an exact count. If either of them is unable to move the number of steps indicated by their toss, they will have to wait until their next turn to try again.  The tortoise reasons that these delays will simulate “naps,” like the nap that the hare took in their original race, according to Aesop’s account

The hare agrees, but then asks, “How many steps long should our racetrack be? If the track is too short, like only 1 or 2 steps, you have the advantage. If the track is very long, I will have the advantage because I will get so far ahead of you that naps won’t matter, and I’ll easily win.”

Problem to Ponder: What length should the racetrack have to make this game fair for both the tortoise and the hare? Note that ties are possible in this race, since the tortoise and the hare move at the same time.

Tortoise and Hare racetrack, with N steps:

More Ponderings:
In our proposed rematch of the Hare and the Tortoise in their famous race recounted in Aesop’s fable, recall that the contestants agreed that the Hare will roll a six-sided number cube and move the number of spaces, from 1 to 6, that show up on the top of the cube. The Tortoise will flip a coin and move 1 space for heads, 2 spaces for tails. To win, a contestant must land by an exact count on the last space of the racetrack. The contestants will toss their cube and coin at the same time. If they can’t move because of the exact count condition, they will “nap” and try again on the next turn. Their dilemma: what should the length of their racetrack be for a fair race under the conditions of this agreement?

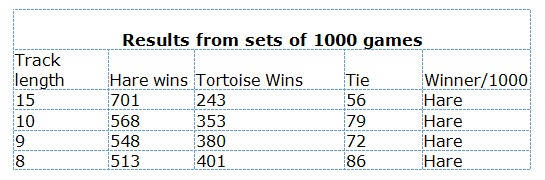
This type of problem lends itself to gathering a lot of data—either through real plays of the game with a cube and a coin or through a computer simulation that does the same thing. The tables below show data from sets of 1000 games simulated for racetracks of different lengths. The data for racetracks of length 15, 10, 9, and 8 show that, for these lengths, the Hare definitely has the advantage. However, it is interesting that even for a racetrack with a length of 15 steps, the Tortoise will still win nearly 25 percent of the games—the “nap” condition actually will allow the Tortoise to catch up, even on longer racetracks.

For very short racetracks, the Tortoise has a big advantage. For example, the data below indicate that for tracks with lengths of only 1 or 2 steps, the Tortoise will win about 73% or 67% of the time, respectively. Track lengths of 5, 6, and 7 steps present an interesting twist. The data show that the Tortoise will win the majority of the races on a track of length 5 for each of three sets of 1000 games. The Hare will win the majority of each of three sets of 1000 races on tracks of length 6. And for races on tracks of length 7, they will split—in the simulated data, each runner had a slight edge in 2 of the 4 sets of 1000 games run on a track of length 7.

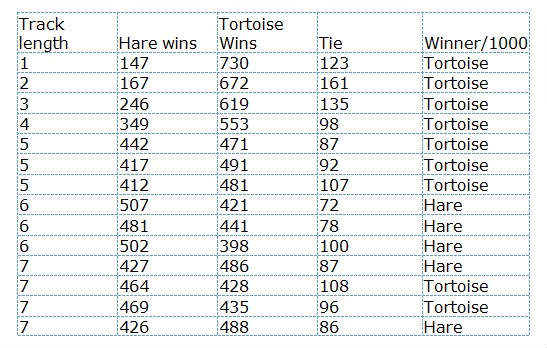
Overall, the Tortoise is favored in races on tracks with lengths ≤ 5. Then a transition in favor of the Hare appears to occur in races on tracks of length 5 to 6. Then, in races on tracks of length 7, the Tortoise and the Hare seem to be nearly evenly matched. Then the Hare is clearly favored in races on tracks with lengths ≥ 8.

Why does the Hare begin to get the advantage in races on tracks of length 6 and then lose that advantage in races on tracks of length 7?

Some ponderings: A track of length 7 is the first racetrack on which the Hare cannot win with one turn— the Hare must take at least two turns to win. A track of length 6 is the first racetrack on which the Hare doesn’t have the chance of a “nap” on the first roll—the Hare can move no matter what number comes up, although the Tortoise will need at least 3 turns to win or tie.

Further ponderings: What would be the theoretical probabilities of a win for the Tortoise, a win for the Hare, or a tie for the two of them, in races on tracks of some of these lengths? For example, for a racetrack of length 1, there are four possible results after just one toss:

1) Both racers move one space, and it’s a tie game.

2) The Tortoise moves 1, and the Hare has to “nap.”

3) The Hare moves 1, and the Tortoise has to “nap.”

4) Both players have to “nap,” because both tossed a result larger than 1.

Remember, both contestants have to land by exact count on that last space.)

The probability the Tortoise wins on the first toss is 1/2 x 5/6 = 5/12.

The probability the Hare wins on the first toss is 1/2 x 1/6 = 1/12.

The probability of a tie on the first toss is 1/2 x 1/6 = 1/12.

The probability that both players “nap” on the first toss is 1/2 x 5/6 = 5/12.

Of course, that’s just on the first toss. If both players “nap,” then we’re really back at the beginning of the race again. Nothing has happened—and on the next toss, the probabilities will again be 5/12 for the Tortoise, 1/12 for the Hare, 1/12 for a tie. Races of longer length involve recursion, since we can use the information already established for races on tracks of shorter lengths at various stages within the races on tracks of longer lengths. Keep on pondering our rematch of the Tortoise and Hare, and we’ll revisit our contestants in future PTP columns.

More Ponderings:

Last month we shared a table of experimental results from 1000 trials for racetracks of various lengths for our rematch of the Tortoise and the Hare. We also noted that if the racetrack were only 1 step long, the Tortoise had a 1/2 x 5/6 = 5/12 probability of winning the race on the first toss, the Hare had a 1/2 x 1/6 = 1/12 probability of winning the race on the first toss, and the chance of a tie on the first toss was also 1/2 x 5/6 = 1/12. (Recall that the Tortoise tosses a coin and moves one step if he tosses heads and two steps if he tosses tails. The Hare tosses a six-sided number cube and moves the number of spaces, 1–6, that it shows). The chance that our game goes on to a second roll—meaning that both contestants have to “nap” on the first roll, is 5/12. Now think about the second roll. If no one wins on the first roll, it is “déjà vu all over again.” On the second roll, the Tortoise again would have a 5/12 chance of winning, the hare would have a 1/12 chance, and there would be a 1/12 chance of a tie.

Consider the numerals that we made bold in the previous sentence. Another way to think about the problem is to consider that on any one turn for the race of length 1, the chances of winning are always in this constant ratio of 5 : 1 : 1, Tortoise wins : Hare wins : tie. Overall, the outcome “space” for the race of length 1 can be thought of as having 5 + 1 + 1, or 7, equal-sized pieces, 5 of which go to the Tortoise, 1 of which goes to the to the Hare, and 1 of which goes to a tie. This suggests that in the long run, the probabilities of winning a race of length 1 are, respectively: 5/7 for the Tortoise, 1/7 for the Hare, and 1/7 for a tie. If we look back at our experimental results for 1000 trials of race length 1, we see that out of 1000 trials,

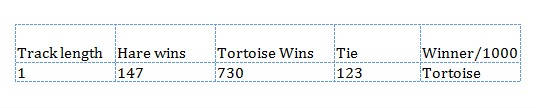
Comparing experimental results with theoretical probabilities, we notice that for the Tortoise, 730/1000 = .73, whereas 5/7 = .714, to three decimal places. Also notice that for the Hare, 147/1000 = .147, whereas 1/7 = .143, to three decimal places. So our experimental results from 1000 simulations of the game lend support to the 5/7, 1/7, 1/7 theory that we have formulated by reasoning about races of length 1.

You can then use this result to help analyze races of length 2. Give it a try. Players either win immediately (Tortoise 5/12, Hare 1/12) or move to a state where one or more of the players are in a game of length 1 for the next roll. In this way, probabilities for winning games of longer lengths can be determined by breaking the game down into cases that use theoretical probabilities that have already been computed for shorter length games—a heavily recursive approach.