Comparing Some Regions in a Square 

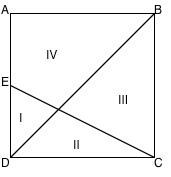
In the figure below, quadrilateral ABCD is a square, and E is the midpoint of the side AD. How do the areas of regions I, II, III, and IV compare?  Another way to think about this is to consider the question, What are the ratios of the areas of the four subdivisions, I : II : III : IV? This problem also has many interesting extensions for your students. For example:

• What happens if E, instead of being the midpoint of AD, is located at the 1/3 mark on segment AD? 
• Suppose that the original figure ABCD is actually a rectangle that is not  a square. Does this change affect the ratios of the respective areas?
  

And you can probably pose some additional extensions of your own.

Solution:  

The July Problem to Ponder (PTP) asked the following question: What are the ratios of the areas of the four subdivisions, I, II, III, and IV in the square below, where E is the midpoint of the side AD? In other words, what is I:II:III:IV?  

Reasoning path 1: Some students start solving this problem by noticing that triangular regions I and III are similar figures (AAA similarity theorem), and since their sides are in a ratio of 1:2, the areas are in a ratio of 1:4 .

Reasoning path 2: Another nice starting observation is that triangular regions I and II have the same altitude from the point of intersection of segments EC and DB to the opposite sides (ED and DC, respectively). However, since base ED is half of base DC, region I has half the area of region II. Because triangles I and II have equal altitudes and their bases are in a ratio of 1:2, their areas will also be in a ratio of 1:2. These two observations can give a really good start on this problem. 

This is a problem that can also be solved by using algebra. Many students will represent this figure in the coordinate plane and then write equations. Sometimes, however, algebraic approaches can make things messier, and this is one of those times. 

More reasoning on this problem will be shared next month. Recall that extensions of this PTP asked (i) what if E were at the 1/3 mark on AD instead of 1/2? and (ii) if ABCD were a non-square rectangle, would that change the ratio of the areas? One might also ask, What if E were at the 1/4 mark? The 1/5 mark? The 1/nth mark on AD?

An Additional Note:

The July Problem to Ponder asked: What are the ratios of the areas of the four subdivisions, I: II: III: IV, in fig. 1 below, where E is the midpoint of the side AD?

Fig. 1 

Two initial reasoning paths were discussed in the August Problem to Ponder column. First, regions I and III are similar figures, and second, the triangles for regions I and II have the same height from the intersection point of DB and EC, but the base of region I (ED) is half the length of the base for region II (DC).

Another interesting approach is to break up the entire square into equal-area triangles, as shown in fig. 2.  The points E, E′, E′′, and E′′′ are the respective midpoints of the sides of the square. This tessellation uses ten copies of region I (see the shaded triangles in fig. 2), and creates two other congruent triangles in regions II and IV. These obtuse triangles have the same area as region I. Thus, region I is 1/12 of the area of the square; the ratio of the areas of regions I: II: III: IV is 1:2:4:5, which can be seen by counting up the number of equal-area triangles within each region.

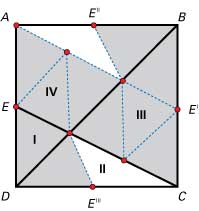
   Fig. 2   

One of the extensions of this problem asks what the ratios of the four subdivisions would be if point E were located at the trisection point of AD instead of at the midpoint. Will the strategy of tessellating by equal-area triangles work to find the ratios of the areas of the four regions in the trisection case? Will the equal-area strategy still work if ABCD is a nonsquare rectangle? Give these extensions a try.