What is the Relationship between Triangles? 

In triangle ABC, segment AG from vertex A meets opposite side BCat a point G, with the length of CG 1/3 the length of BC. That is, point G is located 1/3 of the way along segment BC from C. Similarly, points E and F are located at 1/3 marks along the other two sides of triangle ABC. The intersections of these segments are the vertices of another triangle, IJH, in the interior of triangle ABC.

What is the relationship between the areas of triangles ABC and IJH?

Some Approaches: 

Nowadays, with so many dynamic geometry applications readily available, it is really tempting to investigate this problem with dynamic geometry software to get some idea of how the areas compare by using measuring tools. That will serve to help us make some conjectures, but of course, we would still have to prove our conjectures!
Consider another approach, together with some initial observations on the problem. Sometimes with problems like this one, it is helpful to look for relationships among various triangles and polygonal regions. Just listing things that we do know can sometimes help us to get started. For example, segment AF is 1/3 the length of segment AC, so we know that triangle ABF has 1/3 the area of triangle ABC, because both of these triangles also have the same altitude from point B.

 

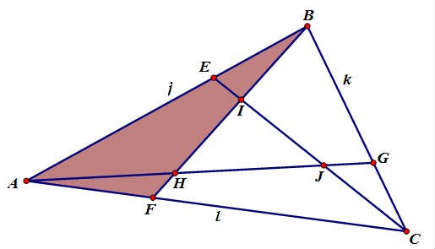
The same is true for triangles AGC and CEB, each of which also has 1/3 the area of the original triangle, ABC. If we shade all three of these 1/3 area triangles, we can see more relationships.

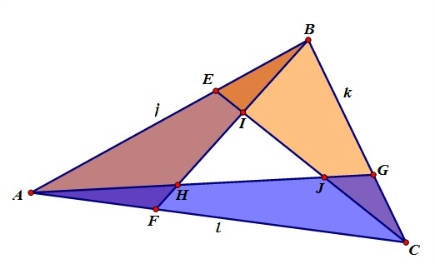
Each of the triangles ABF,CBE, and ACG, has 1/3 the area of triangle ABC, so Area ABF + Area CBE + Area ACG = Area ABC. Furthermore, in the figure above, we see that these three triangles overlap in such a way as to leave the area of triangle IHJuncovered, and the area of triangle IHJis exactly what we are trying to find! Since the areas of ABF, ACG, and CBE doadd up to the area of triangle ABC, the “missing area” in the picture above can be accounted for in the overlap parts, the small triangles AHF, BIE, and CJG, because those are being ”counted twice.” 

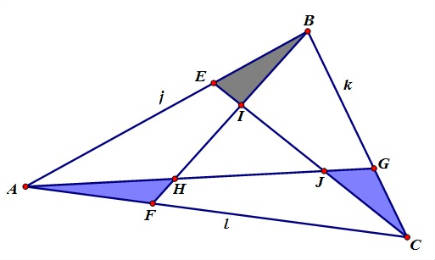
So, now we also know that

Area AHF + Area BIE + Area CJG = Area IJH.

Can you determine anything about the areas of these three corner triangles?

That may be a key to the area of triangle IHJ. Stay tuned…

In last month’s Problem to Ponder discussion, we reasoned that the area of triangle HIJ is equal to the sum of the areas of the three small shaded triangles in figure 2.

Leah Wulfman, a former student of high school teacher Michael Caraco, suggested that if we construct a line through each of the three vertices of the tangled triangle HIJso that each line is parallel to the respective opposite side, we will create “copies” of triangle HIJ, as shown in figure 3.

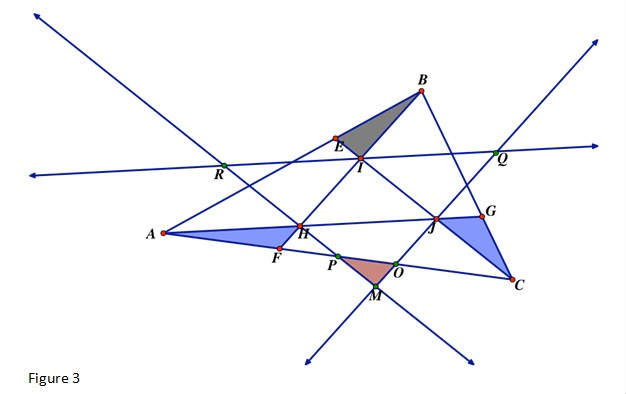
Construct lines through points H, I, and J respectively parallel to opposite sides IJ, HJ, and  HI. This construction yields parallelogram HIJM (opposite sides parallel), and produces four congruent triangles all within a similar triangle RMQ that is formed by the intersections of the three constructed lines. (Note that triangle HIJ is congruent to triangle JMHby SSS, the other two triangles are then congruent by ASA). We need then to find a way to argue that the small triangle OMP, which is exterior to our original triangle ABC, is congruent to triangle FHP. Then we could compose at least four copies of triangle HIJ from regions inside the original triangle ABC.

Because we also know that the three “corner” shaded triangles fill an area equal to a fifth copy of triangle IHJ, at this point we would know that our tangled triangle, HIJ, has an area less than 1/5 the area of our original triangle, ABC.

Only three other pieces inside of triangle ABC remain for us to take into account: triangle OJC and two other unshaded triangles, one with a vertex at A, the other with a vertex at B.