Figuring out Figurate Numbers 
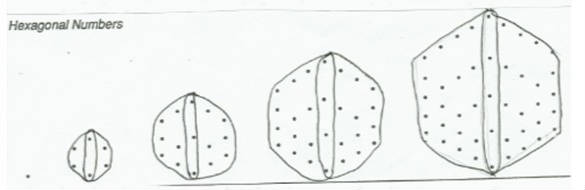
The figure below shows the visual pattern for the first few triangular, square, pentagonal, and hexagonal numbers. These numbers are called figurate numbers. The number of dots in an individual polygonal shape represents a particular figurate number for each pattern. For example, the first five triangular numbers are 1, 3, 6, 10, 15. The first four square numbers are 1, 4, 9, 16, and the first three pentagonal numbers are 1, 5, 12.

The nth square number is n². Each nth triangular number is the sum of the first n positive integers: 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10…. The recursive process of producing this number can be visualized as adding a row of n dots to the top of the previous triangular number to obtain the next one in the pattern. Your students may or may not already know a quick way to find the nth triangular number.

What are the nth pentagonal and hexagonal numbers?
Construct the pattern for the first five heptagonal and octagonal numbers, respectively. What are their nth numbers?

Extension: Can you find a way to represent the nth p-agonal number, where p is the number of sides of a regular polygon?

Some Ponderings: 

Recall that the figure below shows the visual pattern for the first few triangular, square, pentagonal, and hexagonal numbers. These numbers are called figurate numbers. The number of dots in an individual polygonal shape represents a particular figurate number for each pattern. For example, the first five triangular numbers are 1, 3, 6, 10, 15.

a) What are the nth pentagonal and hexagonal numbers?

b) Construct the pattern for the first five heptagonal and octagonal numbers, respectively. What are their nth numbers?

c) Extension: Can you find a way to represent the nth p-agonal number, where p is the number of sides of a regular polygon? 

The nth square number is n². Each nth triangular number is the sum of the first n positive integers: 1, 1 + 2 = 3, 1 + 2 + 3 = 6, 1 + 2 + 3 + 4 = 10…. Your students may already know that the nth triangular number is n(n+1)/2, as suggested by the following:

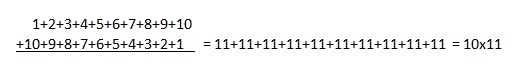
Because this process gives us two copies of the number of dots in the 10th triangular number, we need to divide by 2, so the 10th triangular number is 10x11/2, or 55. Thus, generalizing, we can write the nth triangular number as n(n+1)/2.

Students often approach the challenge of finding representations for other nth figurate numbers by looking for sub-patterns within the collections of dots. Many of the ways to do  lead to considering equivalent expressions that are based on visual patterns. For example, consider the subdivision of  the pentagonal numbers shown below.

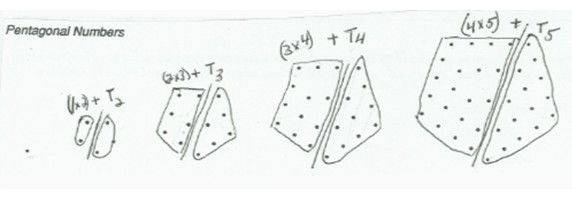
Each pentagonal number is split into a rectangular array and a triangular number, a subdivision that suggests that we can represent the nth pentagonal number by (n-1)n + T_n, where T_n  is the nth triangular number.

So the sub-pattern suggests that the nth pentagonal number can be expressed as P_n = (n-1)n + n(n+1)/2. Many other ways to represent the pattern are possible.

I have seen students subdivide the patterns of dots for the hexagonal numbers into various triangular numbers. For example, consider the subdivisions in the representation below:

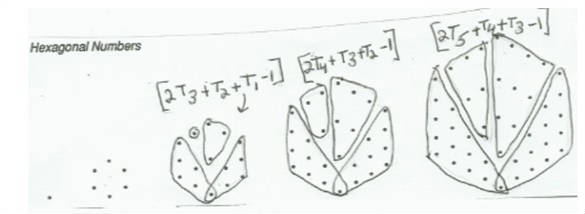
Using this representation, we could write the nth hexagonal number as 2T_n + T_(n-1) + T_(n-2) – 1. The pattern is split up into four triangular numbers, but since there is an overlap of one dot in two of the triangular numbers, we need to subtract 1 for double counting.

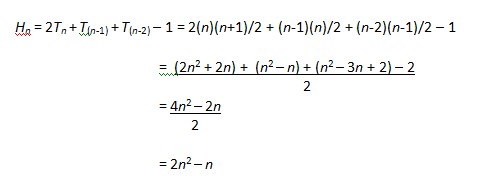
In rewriting an expression for a figurate number pattern, another challenge arises. Can you see a visual pattern for the new equivalent expression? Consider the subdivision of hexagonal numbers below, which indeed suggests that the nth hexagonal number is H_n = 2n² – n.

We’ll return with more ponderings on Figuring out Figurate Numbers in next month’s column!

More Ponderings:  

Recall that the figure below shows the visual pattern for the first few triangular, square, pentagonal, and hexagonal numbers. These numbers are called figurate numbers. The number of dots in an individual polygonal shape represents a particular figurate number for each pattern. For example, the first five triangular numbers are 1, 3, 6, 10, 15.

Last month in our column, we pondered and found general formulas for the nth triangular, square, pentagonal, and hexagonal numbers. We also saw that visual patterns for figurate numbers could be seen in many different ways.

Below, for example, is another way to see the hexagonal figurate numbers, by subdividing them into same-size triangular numbers.

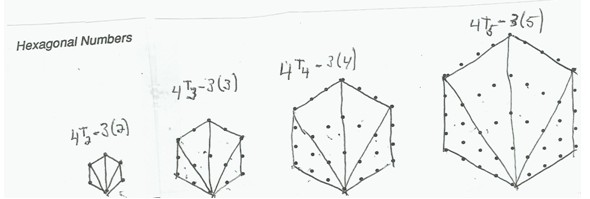
Our illustration shows that the nth hexagonal number contains four copies of the nth triangular number. We then need to subtract the overlap segments of dots of adjacent triangular numbers in the array, since otherwise we would double-count these. This pattern suggests that for the nth hexagonal number, H_n,

H_n= 4T_n  - 3(n)  =  4[n(n+1)/2] – 3n  

= 4n² – 4n   – 3n  = 2n² – n.

          2

Indeed, that is exactly what we obtained last month from a different visual pattern for the nth hexagonal number—that is, H_n  = 2n² – n. 

The extension of our problem asked you to find a way to represent the nth p-agonal number, where p is the number of sides of a regular polygon. We can similarly subdivide other p-agonal figurate numbers into same-size triangular numbers. For example, here is a way to divide the fifth octagonal number into same-size triangular number arrays.

What is the maximum number of nonintersecting regions that we can form by selecting four distinct points on a circle and connecting each pair of them with a chord? By selecting five distinct points? Six distinct points? And of course, then, n distinct points?

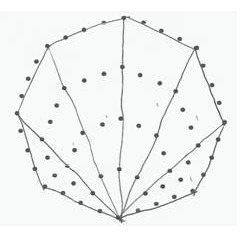
Again, we have to subtract the overlap dots from the adjacent triangular numbers, so working from this representation, we obtain O₅ = 6T₅  - 5(5).  A few more cases of octagonal numbers will convince you that we can generalize this to O_n= 6T_n  - 5(n).

Now it’s your turn to generalize these cases to a representation for the nth p-agonal figurate number!