By Harold Reiter, posted February 27, 2017 —

This blog was inspired by a message from Roger Howe. The earliest known published version of the riddle below comes from a manuscript dated to about 1730 (but differs in referring to nine rather than seven wives). The modern form was first printed circa 1825:

As I was going to St. Ives,

I met a man with 7 wives.

Each wife had 7 sacks.

Each sack had 7 cats.

Each cat had 7 kits.

Kits, cats, sacks and wives,

How many were going to St. Ives?

The rhyme is generally thought to refer to St. Ives, Cornwall, when it was a busy fishing port and had many cats to stop the rats and mice from destroying the fishing gear. Some people argue that it refers to St. Ives, Huntingdonshire, an ancient market town.

Because only the riddle’s poser is “on his way” to St. Ives, the trick answer is 1. But if we leave out the speaker, the intention is to ask the sum

7 + 7² + 7³ + 7⁴.

Rather than simply crunching the numbers on a calculator, a teacher might write this:

Let S denote the sum we seek. Then compute 7S. Next consider 7S – S:

7S – S = 7² + 7³ + 7⁴ + 7⁵ – (7 + 7² + 7³ + 7⁴)

            = 7⁵ + 7⁴ – 7⁴ +7³ – 7³ +7² – 7² – 7

            = 7⁵ – 7 = 7(7⁴ – 1)

            = 7(7² – 1)(7² + 1)

            = 7 · 48 · 50 = 6 · 2800

So S = 2800. Adding the speaker, we get 2801 “things” going to St. Ives. Where is the algebra? So far, there isn’t any. But replace the integer 7 with the letter x, and consider xS – S:

xS – S = x² + x³ + x⁴ + x⁵ – (x + x² + x³ + x⁴)

            = x⁵ + x⁴ – x⁴ + x³ – x³ + x² – x² – x

            = x⁵ – x = x(x⁴ – 1)

            = x(x² – 1)(x² + 1)

This leads to the surprisingly lovely formula

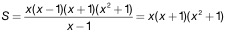
Now we have a solution to any of the possible variations of the riddle; we can replace x with any value, say 9, as in the original riddle. A teacher who is aware that students are eventually going to need to understand the second general solution can pave the way by discussing the specific case first.

Similarly, the finite geometric series

S = a + ar + ar² + ... + arⁿ

leads to

rS – S   = r(a + ar + ar² + ... + arⁿ) – (a + ar + ar² + ... + arⁿ)

            = arⁿ⁺¹ – a

and S = (ar ⁿ⁺¹ – a)/(r – 1).

In the case where ΙrΙ < 1, we have rⁿ⁺¹ → 0 as n→∞, so the infinite series converges, and we have S = a/(1 – r).

As another extension, consider the series for which the nth term is n/2ⁿ. Multiply the infinite sum

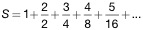
  by 1/2 to get

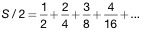
and subtract to get

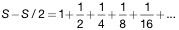
which we recognize is just 2. Hence, our original sum is S = 4.

Even a third-grade teacher with a firm math background can present the arithmetic in a children’s poem in such a way that students later recognize the beautiful ideas associated with a geometric series.

Harold Reiter has taught mathematics for more than fifty-two years. In recent years, he has enjoyed teaching at summer camps, including Epsilon, MathPath, and MathZoom. His favorite current activity is teaching fourth and fifth graders two days each week.