Two Ways to Pay for Class Party Juice Boxes
Grades:
3rd to 5th
Periods:
1
Author:
Tutita M. Casa, Kathryn O'Connor, and Emma Dearborne
All materials should be placed where students can easily access them should they decide to use them at any time after the teacher presents the task.
- Assorted manipulatives, such as base-ten blocks, inch tiles, linking cubes, and money
- Materials to support exploratory writing (Casa et al. 2016; Firmender, Casa, and Colonnese 2017)
- Various writing utensils (e.g., colored pencils, highlighters)
- Different types of paper (e.g., scrap paper, sticky notes, graph paper)
- Juice box carton (optional)
The following context is based on the class party scenario the authors presented in “
Inquiry + Math Workshop Model = Student Centered Success!” (O'Connor, Dearborne, and Casa 2021). Teachers are encouraged to identify another similar context-
such as a field trip where someone authentically will need to purchase drinks or food for the class-that calls for students to “multiply a whole number of up to four digits by a one-digit whole number [or] multiply two two-digit numbers” (CCSSI 2010, p. 29).- Share with the class that you plan to have a class party and purchase juice boxes. Ask students to share what they know about the cartons they come in, and possibly show them one. What do they notice about how many come in the carton?
- Have some students talk about whether their thirst was quenched with just one juice box. Chances are that at least one student says they typically need to drink two. Therefore, you plan to make sure they each have at least two juice boxes during the class party. If you have the time, have the class engage in a conversation about how many cartons students think they'll need. First have individuals or pairs problem solve and then share their ideas with the class. Otherwise, you can tell students the number you will purchase, which should match the number of students in your class. (In our article, we presented a case for purchasing four cartons.)
- Let them know that you need their help figuring out how much it would cost to buy the four juice box cartons that are on sale for $8.25. To be sure that they determine an accurate cost, partners should find two different ways to solve the problem. They should be prepared to convince the class why their solution is a valid one.
- While partners work, ask such conferencing questions as those listed in figure 4: “Why did you do that? Can you explain more?” (p. 193) to understand students' thought process. Also pose such questions as “What are you struggling with?” (p. 193) to support students who may be struggling. Use the conferencing activity sheet pictured in figure 3 to record your observations of each pair's progress. Rely on the discourse tools outlined in figure 6 (p. 194) to advance students' understanding.
- Have partners prepare to share their ideas with the class. Their task is to convince others not only that their answer is correct, but also that their solution is mathematically valid. Ask questions such as “What do other people need to know in order to follow your reasoning?” (p. 193) to help them plan how to communicate with others.
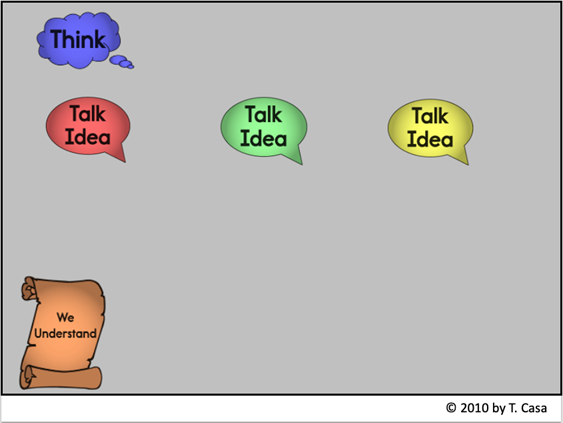 Bring the class back together to have partners share their solutions. Using 5 Practices for Orchestrating Productive Mathematics Discussions (Smith and Stein 2011), sequence the discussion to make purposeful choices about the order in which student work is shared. One way to have students organize their thinking is to use a talk frame (Casa 2013), which is a graphic organizer that teachers use to capture the class discussion on the board. The image seen here is a sample talk frame representing the organization of a talk frame that would have three main ideas. In practice, the number of Talk Idea icons depend on the thoughts shared by students and how the teacher decides to organize notes reflecting the class discussion.
Bring the class back together to have partners share their solutions. Using 5 Practices for Orchestrating Productive Mathematics Discussions (Smith and Stein 2011), sequence the discussion to make purposeful choices about the order in which student work is shared. One way to have students organize their thinking is to use a talk frame (Casa 2013), which is a graphic organizer that teachers use to capture the class discussion on the board. The image seen here is a sample talk frame representing the organization of a talk frame that would have three main ideas. In practice, the number of Talk Idea icons depend on the thoughts shared by students and how the teacher decides to organize notes reflecting the class discussion.
a. For the Think section, have students state in their own words what the task asked them to figure out.
b. Either record partners' ideas in the Talk Idea section or have several pairs that you observed having alternative approaches come up to the board to share one or both strategies.
c. Summarize the class learning in the We Understand section. For this problem, students should conclude that you will need to pay $33 to purchase four juice box cartons. One anticipated solution would be to decompose $8.25 as $8 and $0.25, then reason that since 8 x 4 = 32 plus four quarters, each worth 25¢, or $1 altogether, the total adds to $33.
Assessments
Use the conferencing activity sheet (figure 3, p. 193) to record observations of students' progress and areas of struggle, including if they were able to resolve them during their partner work. Update your notes when students present their ideas to the class. The talk moves listed in figure 5 (p. 194) can allow you to better comprehend the depth of students' understanding, encourage continuous reasoning, and position them to determine valid mathematical ideas. If using a talk frame to facilitate a whole-class discussion, a photograph of the completed one can serve as an additional piece of evidence as you engage in the formative assessment process that can inform future instruction.
Extensions
Ask the class to help calculate the cost of other party items, such as the food, or ask students to increase the number of cartons needed to accommodate an entire grade level. Have them write an informative/explanatory or argumentative (see Casa et al. 2016; Firmender, Casa, and Colonnese 2017) letter to volunteers, such as parents or community members, who have agreed to purchase the items for the party.
A further extension would be to ask students to create a small poster explaining their thinking. Have them present their solution to the class using the poster as a way to communicate rather than the teacher facilitating a discussion. Students also could go on a gallery walk where pairs can leave feedback for each other on their solutions.
- What approaches might be ones you expect students to initially consider?
- What are some challenges that you anticipate students will have?
- How might you pair students who are at a similar level so that they can both be positioned to reason and communicate mathematically rather than one taking the lead?
- With respect to SMP 1, how do you envision students making sense of the problem? What might they readily realize, and what might they find challenging?
- With respect to SMP 3 and 6, how might you encourage students to respond to the partners who are presenting to the class? (See the discourse tools provided in figure 6 and accountability during discussions guidelines presented in figure 7 for suggestions.)
Learning Objectives
Students will be able to identify various strategies to multiply a three-digit number by a one-digit number.
Students will be able to defend their solution strategies.
Common Core State Standards for Mathematical Content
CCSS.MATH.CONTENT.4.NBT.B.5: Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models (CCSSI 2010, p. 29).
Common Core State Standards for Mathematical Practice (CCSSI 2010, pp. 6-7).
SMP 1. Make sense of problems and persevere in solving them.
SMP 3. Construct viable arguments and critique the reasoning of others.
SMP 6. Attend to precision.