In our first editorial (Cai et al., 2017), we highlighted the long-standing, critical issue of improving the impact of educational research on practice. We took a broad view of impact, defining it as research having an effect on how students learn mathematics by informing how practitioners, policymakers, other researchers, and the public think about what mathematics education is and what it should be. As we begin to dig more deeply into the issue of impact, it would be useful to be more precise about what impact means in this context. In this editorial, we focus our attention on defining and elaborating exactly what we mean by “the impact of educational research on students’ learning.”
Within the educational research community, impact on students has been conceptualized and measured in many ways. For example, sometimes impact on students has been examined by looking for gains on standardized test scores. Other times, impact has been examined through gains on measures using open-ended tasks. Sometimes impact on students has been measured by economic indicators, such as students’ later-life earnings, or by the contributions individual students make to society. Impact can also be defined as empowering students to change aspects of their communities or society to be more just and equitable (e.g., Martin, Anderson, & Shah, in press).
As in the first editorial (Cai et al., 2017), we do not claim to have a monopoly on the correct characterization of the impact of educational research on students’ learning. However, we do believe that the field has sometimes been narrowly focused on particular kinds of impact. As educational researchers, a natural question to ask is how our research can have not only a greater impact on student learning but also a broader impact. We start by sharing findings from a study that sparked our thinking—an article by Lindqvist and Vestman (2011) illustrating the effects of both cognitive and noncognitive abilities on individuals’ lives.
A Longitudinal Study of Labor Market Success
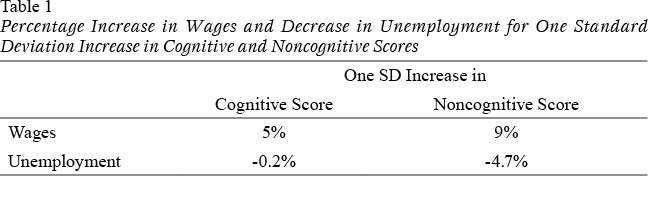
In a longitudinal study of over 14,000 men in Sweden, Lindqvist and Vestman (2011) found evidence that the men’s success in the labor market, defined by their employment rates and annual earnings, correlated with both their cognitive and their noncognitive abilities. Lindqvist and Vestman examined data from cognitive and noncognitive measures for male Swedish military enlistees as well as subsequent labor market data for these individuals. The enlistees underwent a comprehensive, compulsory military enrollment process when they were 18 years old, with cognitive ability measured by a four-part military-constructed test and noncognitive ability measured by a composite score produced from an individual interview with a certified psychologist. The composite score on noncognitive ability consisted of ratings on characteristics such as social skills, emotional stability, and persistence. Labor market data spanning the subsequent 20 years was obtained via tax returns and unemployment compensation rates.
The study’s findings showed that cognitive ability, though a significant predictor of success in the labor market, was hardly the sole factor. Noncognitive abilities were also shown to affect future labor market success; in fact, the overall impact of noncognitive abilities was greater than that of cognitive abilities. For example, a one standard deviation increase in noncognitive score measured at age 18 predicted a 9% increase in wages 20 years later, compared with only a 5% increase in wages associated with a one standard deviation increase in cognitive score (see Table 1). Similar differences held for unemployment (a 4.7% decrease vs. a 0.2% decrease). Although these differences might appear numerically small, they reflect a significant impact.
Looking for Research Impact on What?
Of course, labor market measures do not constitute a full definition of success. We use them here for illustrative purposes to make a point, which is that the field would benefit from broadening its collective conception of what it means for research to have an impact on students.
Given our goal of elaborating what we mean by impact, we suggest that this study by Lindqvist and Vestman (2011) conveys at least two salient messages. The first message lies right at the surface: When we consider impact on students’ learning, we must not neglect the broad view of the kind of learning we are targeting. When targeting and measuring impact, researchers need to consider noncognitive as well as cognitive variables. In the past two decades, attention to noncognitive factors, both as predictors and as learning outcome measures, has increased in the field of mathematics education research (Middleton, Jansen, & Goldin, in press). Looking outside of mathematics education, a number of recent studies have suggested the importance of noncognitive abilities in predicting a wide range of life outcomes, including educational achievement, labor market outcomes, health, and tendency to criminality (e.g., Kautz, Heckman, Diris, ter Weel, & Borghans, 2014; Roberts, Kuncel, Shiner, Caspi, & Goldberg, 2007). In PISA, student outcomes are assessed not only through measures of achievement but also through measures of noncognitive aspects such as self-concept, self-efficacy, and perseverance. Yet there is still room for progress. Indeed, looking across the research reports and brief reports that have appeared in JRME over the past 20 years, only 10% have attended to noncognitive aspects of students’ experiences.
A second message we can take from Lindqvist and Vestman (2011) is that impact need not be measured exclusively through short-term outcomes such as grades and other immediate achievement measures. Impact can also be measured using long-term outcomes. If a key purpose of education is to prepare students to succeed in the paths they choose to take, we must look beyond the outcomes directly proximal to the use of curricula and instruction informed by our research. As a start, we might consider how we can look beyond the grade bands in which research-based curricula are implemented. For example, the LieCal Project studied both the effects of the Connected Mathematics Project (CMP) in the middle grades while it was being used as well as the effects of the curriculum through the end of high school (Cai et al., 2013; Cai, Wang, Moyer, Wang, & Nie, 2011).
The reasoning behind looking further ahead in the LieCal Project was motivated by research studies on the effectiveness of problem-based learning (PBL) with medical students (Dochy, Segers, Van den Bossche, & Gijbels, 2003; Hmelo-Silver, 2004). In that setting, researchers found that PBL students performed better than non-PBL (e.g., lecturing) students on clinical components in which conceptual understanding and problem-solving ability were assessed. However, PBL and non-PBL students performed similarly on measures of factual knowledge. When these same medical students were assessed again 6 months or a few years later, the PBL students performed better than the non-PBL students not only on clinical components but also on measures of factual knowledge (Vernon & Blake, 1993). An implication of this result is that the conceptual understanding and problem-solving abilities learned in the context of PBL appeared to facilitate the retention and acquisition of factual knowledge over longer time intervals.
Given that the CMP curriculum could also be characterized as a problem-based curriculum, it made sense to investigate whether analogous long-term results might hold with CMP students. Indeed, the LieCal Project found that CMP students had significantly higher mean scores on the 10th-grade state test than non-CMP students, regardless of the covariables used. In addition, CMP students tended to pose more mathematically complex problems and use more abstract problem-solving strategies than non-CMP students when they were in the 11th and 12th grades (Cai, 2014; Cai et al., 2013).
In the past, there have been cases where mathematics education researchers have given some attention to long-term effects through longitudinal studies. For example, Fuson (1997) followed one class of students using an experimental curriculum through first and second grades, documenting changes in their arithmetical thinking over time. Biddlecomb and Carr (2011) studied the development of number concepts in 206 children as they progressed from second grade through fourth grade. Educational psychologists focusing on developmental disabilities in mathematics have also conducted longitudinal studies (e.g., Geary, 2010; Jordan, Hanich, & Kaplan, 2003). With respect to teachers, Fennema et al. (1996) followed 21 primary grade teachers over 4 years of Cognitively Guided Instruction teacher development, looking for changes in the teachers’ beliefs and instructional practices related to building on children’s mathematical thinking. Yet, overall, there have been even fewer reports of longitudinal work published in JRME in the past 20 years than studies involving noncognitive factors—only about 6% of the research reports and brief reports involved longitudinal components.
Despite the examples presented above, the field needs to look at long-term impacts far more than has been done before (Shanley, 2016). This is true for both cognitive and noncognitive factors and outcomes. Of course, longitudinal studies are not a panacea; in addition to the technical and methodological difficulties they pose, such studies will not by themselves help us increase the impact of research on students. Nevertheless, opening the field’s collective eye to see more broadly and further into the future when looking at outcomes is an important step in the ongoing effort to improve the impact of research on students.
Reconsidering the Educational Goals
Broadening the impact of educational research on students to include cognitive and noncognitive abilities requires clarifying the educational goals we hope to achieve in the first place. Educational goals must be defined before research is conducted in support of those goals. It is useful to note that the most broadly stated goals in mathematics education, as contained in national standards documents, include both cognitive and noncognitive goals. In 1989, for example, the National Council of Teachers of Mathematics’ (NCTM) curriculum standards set five goals, two of which were noncognitive (that students “learn to value mathematics” and “become confident in their ability to do mathematics”). The remaining three were cognitive (that students “become mathematical problem solvers,” “learn to communicate mathematically,” and “learn to reason mathematically”). More recent standards documents, like NCTM’s Principles to Action (2014) and the Common Core State Standards for Mathematics (CCSSM; National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010) also identify both kinds of goals. CCSSM, for example, integrates cognitive and noncognitive goals in the Standards for Mathematical Practice. The very first standard is “Make sense of problems and persevere in solving them,” identifying both a cognitive and noncognitive aspect to the standard.
We interpret the inclusion of cognitive and noncognitive goals in the major standards documents as a sign that the field recognizes the importance of these goals. The challenge for the research community is to address the full range of goals judged by stakeholders to have value. If the impact of research is to increase, a starting premise is that researchers must take seriously all types of learning goals when creating and testing hypotheses about the learning opportunities needed to help students develop this full range of mathematical competencies.
As we shift in future editorials from discussing what goals should be targeted to how to help students achieve these goals, our focus will shift from identifying the learning goals of most value (and shown to matter in the long run) to investigating the learning opportunities needed for students to achieve those goals. Now that we have broadened the answer to the question “looking for research impact on what?” we will begin exploring answers to the question “looking for research impact of what?” As a foretaste of that discussion, consider recent research showing that noncognitive characteristics such as persistence, grit, and a growth mindset can affect students’ learning in significant, long-lasting, and powerful ways (Boaler, 2016; Duckworth & Yeager, 2015; Dweck, 2006; Farrington et al., 2012). If the mathematics education community routinely measured particular noncognitive variables deemed important to mathematics learning and to learning in general, it would be possible to look across studies to develop general findings related to those variables as well as to understand how they might be harnessed to attain both cognitive and noncognitive mathematics learning goals. Future editorials will examine approaches, some unconventional, to conducting and reporting impactful research of the conditions under which students can achieve this broader range of goals.
References
Biddlecomb, B., & Carr, M. (2011). A longitudinal study of the development of mathematics strategies and underlying counting schemes. International Journal of Science and Mathematics Education, 9(1), 1–24. doi:10.1007/s10763-010-9202-y
Boaler, J. (2016). Mathematical mindsets: Unleashing students’ potential through creative math, inspiring messages and innovative teaching. New York, NY: Jossey-Bass.
Cai, J. (2014). Searching for evidence of curricular effect on the teaching and learning of mathematics: Some insights from the LieCal project. Mathematics Education Research Journal, 26(4), 811–831. doi:10.1007/s13394-014-0122-y
Cai, J., Morris, A. B., Hwang, S., Hohensee, C., Robison, V., & Hiebert, J. (2017). Improving the impact of educational research. Journal for Research in Mathematics Education, 49(1), 2–6.
Cai, J., Moyer, J. C., Wang, N., Hwang, S., Nie, B., & Garber, T. (2013). Mathematical problem posing as a measure of curricular effect on students’ learning. Educational Studies in Mathematics, 83(1), 57–69. doi:10.1007/s10649-012-9429-3
Cai, J., Wang, N., Moyer, J. C., Wang, C., & Nie, B. (2011). Longitudinal investigation of the curricular effect: An analysis of student learning outcomes from the LieCal Project in the United States. International Journal of Educational Research, 50(2), 117–136. doi:10.1016/j.ijer.2011.06.006
Dochy, F., Segers, M., Van den Bossche, P., & Gijbels, D. (2003). Effects of problem-based learning: A meta-analysis. Learning and Instruction, 13(5), 533–568. doi:10.1016/S0959-4752(02)00025-7
Duckworth, A. L., & Yeager, D. S. (2015). Measurement matters: Assessing personal qualities other than cognitive ability for educational purposes. Educational Researcher, 44(4), 237–251. doi:10.3102/0013189X15584327
Dweck, C. S. (2006). Mindset:The new psychology of success. How we can learn to fulfill our potential. New York, NY: Ballantine Books.
Farrington, C. A., Roderick, M., Allensworth, E., Nagaoka, J., Keyes, T. S., Johnson, D. W., & Beechum, N. O. (2012). Teaching adolescents to become learners. The role of noncognitive factors in shaping school performance: A critical literature review. Chicago, IL: University of Chicago Consortium on School Research.
Fennema, E., Carpenter, T. P., Franke, M. L., Levi, L., Jacobs, V. R., & Empson, S. B. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27(4), 403–434. doi:10.2307/749875
Fuson, K. C. (1997). Snapshots across two years in the life of an urban Latino classroom. In J. Hiebert et al. (Eds.), Making sense: Teaching and learning mathematics with understanding (pp. 129–159). Portsmouth, NH: Heinemann.
Geary, D. C. (2010). Missouri longitudinal study of mathematical development and disability. British Journal of Educational Psychology Monograph Series, II(7), 31–49. doi:10.1348/97818543370009X12583699332410
Hmelo-Silver, C. E. (2004). Problem-based learning: What and how do students learn? Educational Psychology Review, 16(3), 235–266. doi:10.1023/B:EDPR.0000034022.16470.f3
Jordan, N. C., Hanich, L. B., & Kaplan, D. (2003). A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties. Child Development, 74(3), 834–850. doi:10.1111/1467-8624.00571
Kautz, T., Heckman, J. J., Diris, R., ter Weel, B., & Borghans, L. (2014). Fostering and measuring skills: Improving cognitive and non-cognitive skills to promote lifetime success (Working Paper No. 20749). Cambridge, MA: NBER. doi:10.1787/5jxsr7vr78f7-en
Lindqvist, E., & Vestman, R. (2011). The labor market returns to cognitive and noncognitive ability: Evidence from the Swedish enlistment. American Economic Journal: Applied Economics, 3(1), 101–128. doi:10.1257/app.3.1.101
Martin, D. B., Anderson, C. R., & Shah, N. (in press). Race and mathematics education. In J. Cai (Ed.), Compendium for research in mathematics education. Reston, VA: National Council of Teachers of Mathematics.
Middleton, J. A., Jansen, A., & Goldin, G. A. (in press). The complexities of mathematical engagement: Motivation, affect, and social interactions. In J. Cai (Ed.), Compendium for research in mathematics education. Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author.
National Governors Association (NGA) Center for Best Practices & Council of Chief State School Officers (CCSSO). (2010). Common Core State Standards for Mathematics. Washington, DC: Author.
Roberts, B. W., Kuncel, N. R., Shiner, R., Caspi, A., & Goldberg, L. R. (2007). The power of personality: The comparative validity of personality traits, socioeconomic status, and cognitive ability for predicting important life outcomes. Perspectives on Psychological Science, 2(4), 313–345. doi:10.1111/j.1745-6916.2007.00047.x
Shanley, L. (2016). Evaluating longitudinal mathematics achievement growth: Modeling and measurement considerations for assessing academic progress. Educational Researcher, 45(6), 347–357. doi:10.3102/0013189X16662461
Vernon, D. T., & Blake, R. L. (1993). Does problem-based learning work? A meta-analysis of evaluative research. Academic Medicine, 68(7), 550–563. doi:10.1097/00001888-199307000-00015