Examining Equitable Teaching Using the Mathematics Teaching Framework
May 2019
NCTM identified a core set of eight research-informed effective teaching practices in Principles to Actions: Ensuring Mathematical Success for All (NCTM 2014). While the list provides a common professional language for discussing important elements of teaching, it is the interconnections among the teaching practices that support equitable teaching. The authors of the Taking Action Series developed the Mathematics Teaching Framework diagram (shown below) to illustrate how the eight teaching practices form a coherent framework for equitable and ambitious teaching of mathematics (Boston, Dillon, Smith, and Miller 2017, p. 215; Huinker and Bill 2017, p. 245; and Smith, Steele, and Raith 2017, p. 194).
The Mathematics Teaching Framework allows us to explore the intersections between authority, mathematical identity, and mathematical agency with the eight teaching practices. The framework provides us the space to examine equitable teaching as an intentional act that teachers pursue through teaching practices that help them to view each and every student as capable of doing mathematics. I believe that each and every student is mathematically competent and is able to learn high-level mathematics and that equitable teaching opens up interactional space for a broad range of teaching and learning ideas.
I will use the brief vignette below as the context for examining ways students become positioned with authority by linking it to the Mathematics Teaching Framework. Our instructional goal must be to not only support students in developing deep conceptual understanding of mathematics but to also support students in developing identities as knowers and doers of mathematics by building their sense of agency. Too often, authority in mathematics classrooms lies primarily with the teacher or curriculum in which students are compelled to accept without question the mathematical ideas and understandings of these resources. That is, students rarely develop their own ideas, engage in discourse in which ideas are exchanged, or question the reasoning of the ideas presented to them. In classrooms where authority is shared, we find that teachers create opportunities for students to take ownership of their ideas and question the reasoning of concepts presented, resulting in students with a shared understanding of the mathematical ideas and a positive identification with mathematics.
Task: You have two bags containing blue and red gumballs. Bag A contains 6 blue gumballs and 9 red ones, and Bag B contains 10 blue gumballs and 15 red ones. From which bag would you have the better chance of selecting a blue gumball and why?
A teacher plans to use the gumball task to focus on the mathematics learning goal of understanding that equivalent ratios can be created by iterating or partitioning a composed unit. The task supports establishing a foundation of conceptual understanding while promoting student reasoning and problem solving. While planning the lesson, the teacher anticipates several strategies students might use and develops purposeful questions to move students’ thinking forward and to clarify the reasoning behind their ideas. After launching the task, she monitors the class, observing student strategies while posing probing questions to ensure students struggle productively in making sense of the mathematics. After students work individually, she invites students to share their ideas in pairs. The pairs explain their representations and justify their strategies to each other and work collaboratively to resolve any discrepancies and to clarify approaches in anticipation of sharing with the whole class. The teacher then orchestrates whole-class discourse grounded in the work of a pair of students she selected on the basis of the representations and strategies they used. As the pair presents their thinking, the teacher invites other students to revoice, restate, and paraphrase ideas made by the student presenters. Also, she asks other students to connect their own mathematical ideas to the ideas presented in the classroom. Throughout this discussion, the teacher asks purposeful questions of the presenters and of the whole class to make connections among the various representations and strategies used so that the students all reason together about equivalent ratios.
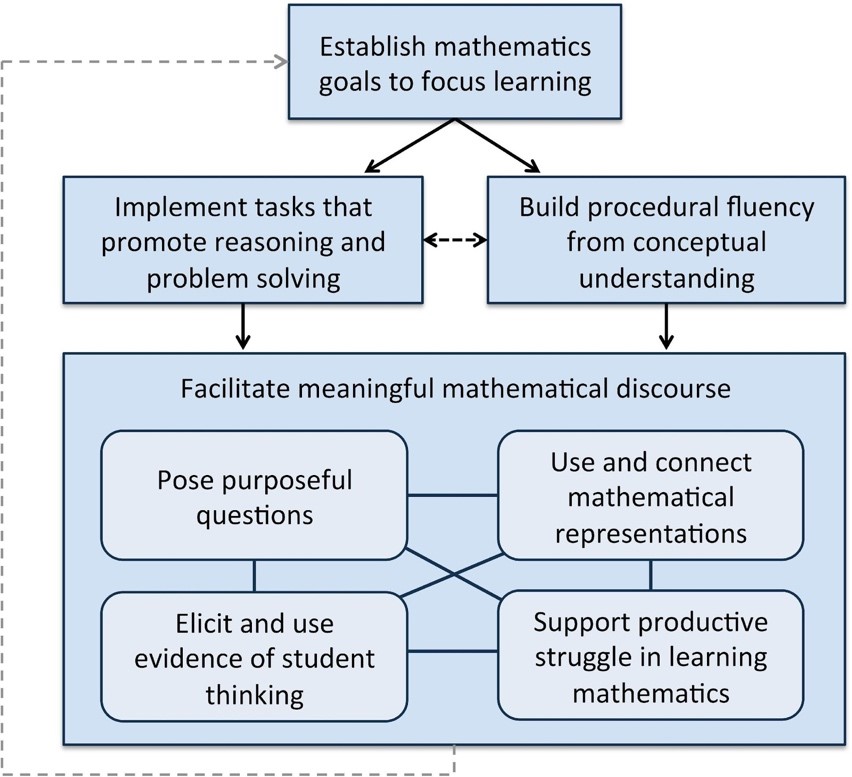
Mathematics Teaching Framework
Establishing classroom goals to focus learning should not only include goals that describe what students are to know and understand about a mathematics topic but should also include norms for participation. Establishing norms for participation acknowledges that student participation is a practice for sharing authority and building agency. In the vignette, authority is shared in the ways students are given space to author their mathematical ideas and given opportunities to explain and justify their representations. Establishing norms that support student engagement positions students as competent in discussing and making sense of their mathematical ideas whether working in pairs, small groups, or as a whole class. This also builds students’ mathematical agency.
Implementing tasks that promote reasoning, problem solving, and conceptual understanding helps students see themselves as doers and sense makers of mathematics. The types of tasks in which students engage shape their view of mathematics and, ultimately, their view of themselves in relation to mathematics. When students engage in tasks that promote understanding, reasoning, and problem solving, they see doing mathematics as such. Consequently, they see themselves as competent in engaging in reasoning and problem solving and making sense of mathematical ideas. Conversely, when students only engage in tasks that focus on using explicitly taught procedures, they see mathematics primarily as recalling ways to find solutions. The task in the vignette asks students to not only generate varied strategies but to also explain and justify their solution. This allows students to draw on the knowledge and resources they bring to the task while also providing the space for students to connect and learn from others’ mathematical ideas.
Building procedural fluency from conceptual understanding provides students with a wide range of options for entering a task and building mathematical meaning. It is plausible that in the task from the vignette, students could create drawings, create a table, act out the task, or find an equivalent ratio. All of these entry points can be valid ways for engaging with the task but they also serve as opportunities to support making connections among these entry points. A teacher might anticipate these entry points as a way to build connections as well as to position the author of the ideas as mathematically competent.
The teaching practices within “facilitate meaningful mathematical discourse” all have implications for strengthening authority, mathematical identity, and mathematical agency. Discourse creates space for students to interact with peers and learn to value multiple contributions, diminishing status. By asking students to revoice, restate, and paraphrase other students’ mathematical ideas, the teacher in the vignette positions students as making valuable contributions and as resources for each other. Students drawing on the connections of others’ ideas situate them in a metacognitive space of thinking deeply about the underlying connections of the mathematics. That is, a student might consider how a drawing of blue and red marbles connects to equivalent ratios in a table. Unpacking these connections through discourse builds students’ sense of agency because they are engaged in sense making, using not only their own mathematical ideas but the ideas of others as well.
The teaching practices within the Mathematics Teaching Framework are a coherent and connected set of practices that when implemented together, create a classroom learning environment supportive of equitable mathematics teaching practices. The questions below are starting points for reflecting on the intersection between the Mathematics Teaching Framework and equitable mathematics teaching practices.
- What are the norms for participation in my mathematics classroom? How are these norms played out in my classroom?
- How do the tasks implemented in my classroom help students see themselves as doers and sense makers of mathematics?
- In what ways do students in my classroom use each other as mathematical resources?
- How do I facilitate discourse in my classroom that communicates to each and every student that their ideas matter?
Robert Q. Berry III
NCTM President
@robertqberry
References
Boston, Melissa D., Frederick Dillon, Margaret S. Smith, and Stephen Miller. 2017. Taking Action: Implementing Effective Mathematics Teaching Practices in Grades 9–12. Reston, VA: National Council of Teachers of Mathematics.
Huinker, DeAnn and Victoria Bill. 2017. Taking Action: Implementing Effective Mathematics Teaching Practices in Grades K–5. Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics (NCTM). 2014. Principles to Actions: Ensuring Mathematical Success for All. Reston, VA: NCTM.
Smith, Margaret S., Michael D. Steele, and Mary Lynn Raith. 2017. Taking Action: Implementing Effective Mathematics Teaching Practices in Grades 6–8. Reston, VA: National Council of Teachers of Mathematics.