Principles to Actions: Ensuring Mathematical Success for All (NCTM, 2014) re-emphasizes the role played by tools and technology as one of six guiding principles for school mathematics, reminiscent of the Professional Standards for Teaching Mathematics (NCTM, 1991) and the Principles and Standards for School Mathematics (NCTM, 2000). In relation to students, the Common Core State Standards in Mathematics (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010) identify students’ ability to use appropriate tools strategically as an important mathematical practice. However, for mathematics teachers to facilitate students’ strategic use of tools, they must consider how to effectively achieve certain mathematical goals through their students’ use of such tools. Helping teachers support students’ use of tools is closely related to several mathematics teaching practices identified in Principles to Actions: establishing mathematics goals to focus learning, implementing tasks that promote reasoning and problem solving, and supporting productive struggle in learning mathematics. However, there are few practical resources available to support mathematics teachers in assessing the role of technology in a given task to enact such teaching practices.
This article details the fourth iteration of an intervention used by the authors to assist preservice and in-service mathematics teachers with using technology in this way. The first three interventions focused on teachers’ ability to utilize a framework designed to help them evaluate and revise Interactive Geometry Software (IGS) tasks (Sherman, Cayton, & Chandler, 2015). However, the intervention described here provided teachers with the opportunity to learn about and make practical use of the IGS Framework (Sherman & Cayton, 2015) to not only evaluate and revise tasks, but also to create interactive geometry tasks with a focus on specific goals for students’ high-level thinking.
Tasks That Support Student Thinking
Research on student learning has demonstrated that students’ mathematical thinking during a task has important implications for student learning. Students who engaged with tasks that required high levels of mathematical thinking demonstrated a greater ability to problem solve, make connections, and communicate their thinking than those who did not (Stein & Lane, 1996). The Mathematical Tasks Framework (Stein & Smith, 1998) distinguishes between three phases that a mathematical task may go through in the process of influencing students’ mathematical learning: the task as written, the task as set up by the teacher, and the task as implemented by students. Research demonstrates tasks that start at a low level during setup virtually always stay at a low level during implementation (Stein, Grover, & Henningsen, 1996). Furthermore, tasks that appear low level as written are not likely to be set up at a high level, minimizing opportunities for student learning. The combination of these issues points to the need to support teachers in their ability to select high-level tasks to provide opportunities to set up and implement at a high level with their students. So what does research have to say about teachers’ ability to select high-level tasks for use in their classrooms?
Research has also demonstrated that the large majority of tasks that teachers select to implement with students are low level. Stigler and Hiebert (2004) shared results of the TIMSS video study, indicating that only 17% of tasks selected by the sample of U.S. teachers were considered high level. Sherman (2014) found that only 26 out of 63 tasks selected by four teachers were initially rated as high-level tasks. However, Boston and Smith (2009) demonstrated that selecting high-level tasks is a skill that teachers can learn. Their results indicated that participants showed statistically significant growth in selecting high-level tasks over the course of a year, as well as selecting high-level tasks more often than a comparison group.
Each of the studies noted above reports results for in-service teachers. Furthermore, only Sherman (2014) addressed the role technology in relation to high-level tasks. As such, we began to wonder how these results might apply to our work with preservice teachers in courses that emphasize the use of IGS. What instructional intervention(s) may assist preservice teachers in selecting or designing high-level IGS tasks for use in their future classrooms? Providing insight into the answer to this question has the potential to increase students’ opportunity to engage in tasks that support their high-level thinking using IGS.
A Framework for Creating Tasks That Support Student Thinking
IGS (e.g., GeoGebra, Geometer’s Sketchpad, Cabri) has been found to support the learning of important mathematics (Hollebrands & Dove, 2011) and students’ mathematical thinking (Sherman, 2014; Cayton, 2012). However, Hollebrands, Laborde, and StraBer (2008) emphasize that research suggests that “the choice of the task in relation to the affordances of the dynamic [or interactive] geometry environment may be critical for the development of the understandings of the students” (p. 174). This statement aligns with our concern that to support students’ strategic use of IGS, teachers must understand not only IGS but also how to capitalize on the affordances of IGS to support students’ thinking. Consequently, we analyzed numerous mathematical tasks that made use of IGS to better understand the role of technology in supporting students’ mathematical thinking.
It is important to note that although the term Interactive Geometry Software contains the word “geometry,” such tools can generally be used to support the learning of a variety of mathematical topics. Indeed, we analyzed tasks that spanned algebra, trigonometry, data analysis, and probability in addition to geometry. Thus, our focus in developing the IGS Framework was not on how IGS can support students’ learning of a particular topic or concept, such as geometry, but how IGS could support students’ high-level mathematical thinking, in general. In this section, we describe the theoretical and research bases that guided the development of the IGS Framework (Figure 1).
An important principle of using technology strategically for mathematics instruction is that the inclusion or exclusion of technology within a given task should depend on the mathematical goals of the task. Only then can a teacher decide which tools, technological, or otherwise may be most effective in accomplishing that goal. Sinclair (2003) describes design principles related to how the sketch (i.e., technological representation of mathematical objects and associated prompts for students’ activity) should depend on the goal of the task. Cayton (2012) examined three teachers’ implementation of preconstructed interactive geometry tasks in Algebra 1 classes and found that all tasks initially rated as high level adhered to these design principles. We use these principles to identify three overarching goals for students’ mathematical activity that correspond to the rows (i.e., dimensions) in Figure 1.
Along each of these dimensions, technology plays a role in achieving the goal. The metaphor of using technology as an amplifier or a reorganizer provides a way to describe the role that technology plays. Pea (1985) used the metaphors of amplifier and reorganizer to distinguish two ways in which technology may be used to support students’ thinking. More specifically, this distinction has also been used to describe the role of technology in mathematics education (Ben-Zvi, 2000; Lee & Hollebrands, 2008; Zbiek, Heid, Blue, & Dick, 2007; Sherman, 2014). One way to describe this distinction is the following:
As an amplifier, technology makes a task more efficient by performing computations and generating representations quickly and accurately, but the nature of what students think about is not essentially changed. As a reorganizer, technology has the capability to transform students’ activity, supporting a shift in students’ mathematical thinking to something that would be difficult or impossible to achieve without it. (Sherman & Cayton, 2015, p. 307).
In terms of the relationship between students’ thinking and the use of technology as an amplifier or a reorganizer, Sherman (2014) found that teachers’ use of technology as a reorganizer was associated with high-level tasks while the use of technology as an amplifier was uncorrelated with the cognitive demand of the task. The results of that study suggest that when technology was used as reorganizer, it was intended to support students’ high level thinking. That is, the use of technology supported a shift in students’ thinking to making generalizations, making connections across representations, or having students interpret and make sense of a novel representation, for example. When used as an amplifier, technology made the task more efficient or accurate, or added “bells and whistles,” but it did not affect the thinking demands of the task.
With respect to the goals above, technology use as a reorganizer is interpreted to mean that the same goals could not be achieved without the use of technology. Thus, once the goal (or goals) of a task is identified, the question is how essential the technology is in helping students achieve that goal. To make this determination, we integrated the design principles with the amplifier/reorganizer distinction into a single framework (Figure 1) to evaluate the role of technology in a given task with respect to each of those goals. Each row represents a different goal, a question is posed to guide the evaluation of the role of technology in relation to that goal, and the use of technology as an amplifier or a reorganizer is described. Note that these goals are not mutually exclusive but are listed separately because the role that technology plays within each varies.
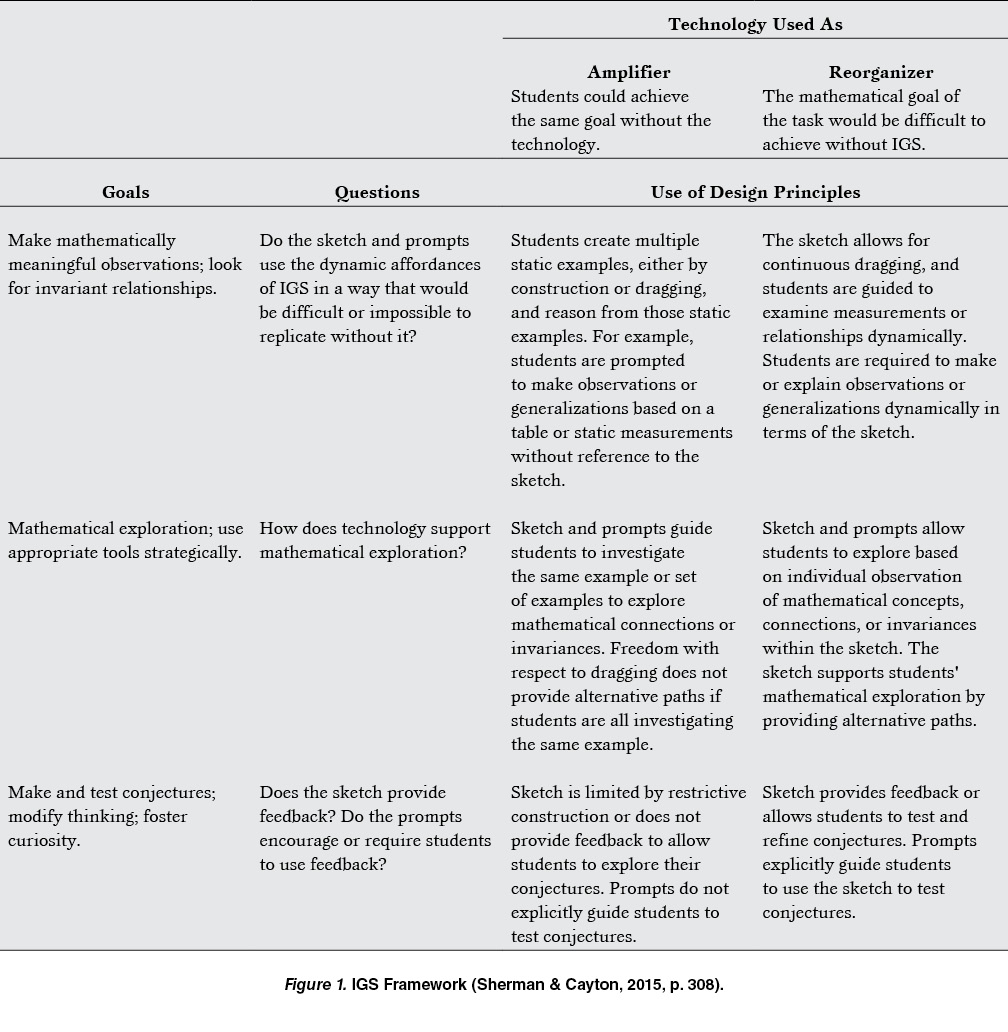
The IGS Framework aims to connect the use of technology with the thinking demands of mathematical tasks and, thus, is necessarily limited in its scope. By drawing on Sinclair’s (2003) design principles and choosing only those principles that are relevant to the written task, we consider only three possible goals for such tasks. Furthermore, the amplifier and reorganizer distinction (Pea, 1985) is only one of many ways to describe the role of technology in mathematical tasks (cf. Zbiek, Heid, Blue, & Dick, 2007). For further details on the development and use of the IGS Framework to evaluate tasks, see Sherman and Cayton (2015). Examples of tasks coded as amplifier or reorganizer along each dimension are provided as appendices (
Appendixes A, B, C).
The Intervention
The intervention was implemented over 3 weeks in a teacher education course at a Midwestern university. The implementation described here was the fourth iteration of using this intervention with PSTs. The class consisted of 22 preservice and one in-service teacher. Fifteen PSTs were pursuing an elementary certification, and the remaining eight were secondary; four PSTs were taking the course for graduate credit while the rest were undergraduates; 20 of the 23 PSTs were female.
There were two broad objectives for the course: (1) to deepen PSTs’ understanding of mathematics through the use of technological tools and (2) to identify issues related to using technology for mathematics instruction and develop strategies for addressing those issues. The first goal was largely remedial in the sense that PSTs generally come into the course with little experience learning mathematics with technological tools and, thus, have limited resources to draw upon in thinking about how technological tools can support the learning of mathematics. Portions of the Preparing to Teach Mathematics with Technology (PTMT) curricula for Data Analysis and Probability (Lee, Hollebrands, & Wilson, 2012) and Algebra (McCulloch, Lee, & Hollebrands, 2015) were used for this portion of the course, which comprised about two thirds of the course.
The intervention described in this article was meant to address the second goal noted above and was implemented as a 3-week sequence at the end of the course, designed to build upon issues related to instruction that were identified and discussed while addressing the first goal. The intervention took place during portions of weekly 2.5-hour class periods over 3 weeks. An overview of the instructional sequence is given in Figure 2. During the 1st week, PSTs were introduced to the IGS Framework and used it to evaluate three tasks (see Appendices A, B, and C), two during class and one for homework. During the second week, PSTs’ evaluation of the third task was discussed, and PSTs worked in groups to revise one of the tasks that they had analyzed during the first week. During the third week, PSTs evaluated and discussed each other’s revisions and shared their ideas for the final project, which entailed using the IGS Framework to design a task. PSTs had approximately 1 week to complete the final project. Further detail about each of these phases of the intervention follows in the next section.
Introducing the Framework
During the first week of the intervention, the IGS Framework (Figure 1) was introduced row by row, emphasizing the goals represented by each row, with examples of tasks that use IGS as an amplifier and a reorganizer for each row (a PowerPoint introduction to IGS Framework for PSTs is provided as
Appendix D). The purpose behind this introduction was to describe the theoretical underpinnings of the framework—the metaphor of using technology as amplifier or reorganizer (Pea, 1985) and Sinclair’s Design Principles (2003)—and then to sufficiently familiarize PSTs with the IGS Framework so that they could use it to evaluate a task.
Analyzing Tasks
PSTs were asked to use the IGS Framework to analyze three tasks in the following order: Intersecting Chords (Saxon Geometry, 2009), Properties of Polygons (Pearson Geometry, 2012), and Midsegment of a Trapezoid (Holt McDougal Larson Geometry, 2012) (Appendixes A, B, and C). The sequencing of these tasks was intentional and was informed by our evaluation of the tasks and observations from previous iterations. In our evaluation of these tasks using the IGS Framework (Sherman & Cayton, 2015), we consider Intersecting Chords to be an amplifier along all three dimensions because (1) the sketch and prompts have students reason from a “drag-and-stop” perspective using the table provided in the student document (Dimension 1); (2) students are told exactly what relationships to explore (Dimension 2); and (3) students are not asked to make or test any conjectures (Dimension 3). Properties of Polygons is considered to be a reorganizer along all three dimensions because the sketch and prompts have students reason dynamically from the sketch while dragging (Dimension 1); students are allowed to construct and explore any polygon they would like (Dimension 2); and students are prompted to make and test conjectures from feedback provided by the sketch (Dimension 3). Midsegments of a Trapezoid is considered to be a reorganizer along the first dimension because students are instructed to use dragging to reason from the sketch; however, this task is an amplifier along the other two because students are told which measurements to take and are given the specific relationship to explore (Dimension 2), and students are not explicitly asked to test their conjecture (Dimension 3). The focus in analyzing these tasks was on the role of technology in achieving the goals as described in each row of the framework and not, per se, on the mathematics.
The way in which we implemented the evaluation of these tasks by PSTs using the IGS Framework was similar for each, and thus we describe in detail how the analysis of the first task, was used to deepen PSTs’ understandings of the distinctions therein. PSTs were given a copy of the Intersecting Chords task (Figure 2) to analyze in groups of three or four, identifying whether the task as written used IGS as an amplifier or a reorganizer with respect to the three goals for students’ thinking represented by each row of the framework: (1) make mathematically meaningful observations, (2) mathematical exploration, and (3) make and test conjectures. PSTs were asked to engage in the task as a student would, using GeoGebra to assess the sort of thinking that was required by the task, and to pay attention to how the task was supported by the use of IGS, using the IGS Framework as a guide.
After 15–20 minutes of engaging with the task and discussing it in groups, a whole-class discussion followed, which was designed to surface differences in how the PSTs interpreted the IGS Framework and to clarify issues raised by discrepancies within or between groups. We first polled groups regarding whether they considered the task to use IGS as an amplifier on a given dimension, and then asked members of these groups to explain their reasoning for that evaluation, followed by the same for reorganizer. After both sides had articulated their reasoning, the teacher educator tried to highlight the point(s) of discrepancy in interpretation between these opposing views, and whether it was a difference in interpretation of the task or the IGS Framework, by asking the class a question that would focus on that difference. In the case of a difference of interpretation of the task, the difference was usually in terms of the wording of the task, and we made no attempt to rule out one interpretation over another but, rather, underscored the idea that how students interpret the prompts will influence how they engage in the task. In the case that the difference in interpretation was about the IGS Framework, we clarified how we intended the wording to be interpreted and applied. In cases where there were no discrepancies with regard to how IGS was used with respect to a given dimension, we still elicited PSTs’ reasoning and discussed it in light of interpreting the IGS Framework in a way that was consistent with our intention.
For example, the second row of the framework is designed to highlight how the use of IGS supports the open-endedness of a task. There are two issues that need to be teased apart in making this evaluation. First, is the task open-ended? Second, does the use of IGS play a role in this open-endedness by providing alternative strategies or pathways for exploration? Quite often, PSTs interpreted this dimension as simply referring to whether or not the task is open-ended without considering the role of technology with respect to this characteristic of the task. The whole-class discussion provided an opportunity to highlight that distinction. Furthermore, there are generally a wide variety of opinions about whether the task is open-ended. The whole-class discussion allowed us to underscore the idea that for our purposes, freedom with respect to dragging alone does not constitute an open-ended task. By providing a brief introduction to the framework and immediately having PSTs use it to evaluate a task, we are able to support PSTs in constructing meaning for this tool and to clarify how to interpret it in the context of applying it to a specific task.
A similar sequence of activities was used to evaluate the Properties of Polygons task, and PSTs’ written work on the analysis of these first two tasks was collected at the end of class. Finally, PSTs were asked to evaluate the third task, Midsegment of a Trapezoid, for homework, which they submitted prior to the next class meeting. The teacher educator examined PSTs’ evaluations and formed groups for the next class based on differences in PSTs’ evaluations. For example, a group of four might be formed by pairing two PSTs that evaluated this task as using IGS as an amplifier on the first dimension with two PSTs that deemed it as using IGS as a reorganizer along this dimension. The main criterion was to group PSTs based on differences without isolating one teacher as differing from everyone else in their group, if possible. The purpose of grouping PSTs in this way was to facilitate discussion about how the PSTs were interpreting the IGS Framework in their application of it to a specific task.
Revising a Task
The IGS Framework has the potential to support mathematics PSTs in the work of teaching by not only using it to evaluate the way in which a given task makes use of IGS to support students’ thinking, but also by suggesting ways in which the task might be revised to make better use of IGS. For example, the Intersecting Chords task asks students to engage in a drag-and-stop action, record static measurements in a table, and reason about the relationships of the mathematical objects represented in the sketch based on these static measurements. This sort of activity aligns well with the description of an amplifier use of IGS with respect to making mathematically meaningful observations. However, the description of reorganizer use of IGS with respect to this goal suggests ways in which the task might be revised to make better use of IGS: “The sketch allows for continuous dragging, and students are guided to examine measurements or relationships dynamically . . . [and] to explain observations . . . dynamically in terms of the sketch.” By describing the way in which this particular task does not make use of IGS, there is the potential for PSTs to gain some insight into how the task might be revised to leverage these affordances.
In addition, revising a task that PSTs had already evaluated seemed to be an important intermediate step between evaluating tasks and designing one, which was what the final project asked them to do. To further support PSTs in making the transition from evaluating to designing tasks, we had PSTs work on revising the Intersecting Chords task in groups. Based on how PSTs had evaluated the Intersecting Chords task originally, they were grouped with 2 or 3 other PSTs who had also deemed this task to use IGS as an amplifier with respect to a given goal, and the group was asked to revise the task with respect to that goal. After PSTs were grouped, their evaluations of the Intersecting Chords task from the previous week were returned to them and they were given directions for making revisions to the task (included as
Appendix E). As part of the revision process, PSTs were asked to identify the mathematical and thinking goals of the task, and how the revisions that they made supported the use of IGS as a reorganizer. Asking PSTs to make their reasoning explicit in this way provided the teacher educator with insight into how PSTs were interpreting, understanding, and using the IGS Framework in the process of making revisions.
PSTs were given about 90 minutes to work in groups on revising the Intersecting Chords task and were asked to submit their revised tasks electronically by the end of class. During this time the teacher educator answered PSTs’ questions about the assignment and assisted PSTs in using GeoGebra to make the revisions that they had decided upon, when necessary. At other times, PSTs had questions about the mathematics—some groups observed that there was a deeper mathematical relationship embedded in the task than the ratio of chord segment lengths, and worked to try to uncover this relationship more explicitly before revising the task. For these groups, the teacher educator tried to guide PSTs’ thinking without simply telling them what some of those relationships were. Ultimately, we wanted PSTs’ revisions to be based on their insights into the mathematics in the task and their ideas about how to use IGS to engage students with that mathematics. Some groups wanted feedback on ideas for revising the task, and in these cases, the teacher educator directed PSTs back to their assessment of the goals of the task and how to best achieve those goals. Again, we wanted PSTs’ revisions to be based on their reasoning about the mathematics and their anticipation of students’ thinking, and not on any perceived authority or expertise of the teacher educator.
Although most groups completed and submitted their revised tasks by the end of class, one or two groups finished and submitted their tasks after class. The teacher educator examined the revised tasks of each of the groups, paired groups who had made revisions with respect to the same goal for the following class (there were a total of six groups, resulting in three pairings, two groups for each goal). Copies of the tasks that each group submitted (minus their reasoning about their revisions) were distributed to the other group, and each group analyzed its paired group’s revised task. The purpose of this exercise was to provide PSTs with the opportunity to (1) use the IGS Framework in analyzing a task that they had previously thought about, and (2) consider other ways of using IGS as a reorganizer to achieve particular goals for students’ mathematical thinking. After each group had the opportunity to evaluate each other’s task, two members from each group swapped groups to discuss their questions about the task with members of the other group and to answer questions about the task they had created. An example of one of the revised tasks created by PSTs is provided as
Appendix F.
Designing a Task
As part of their homework assignment between the second and third weeks of the intervention, PSTs were asked to identify mathematical goals for the tasks that they were to develop for their final projects. PSTs were given the freedom to develop tasks that addressed mathematical topics and grade levels of their choosing. PSTs were asked to write down the goals before they arrived at class, and during class they had the opportunity to share their goals and ideas for their tasks with their groups and to elicit feedback. Finally, PSTs turned in written copies of their mathematical goals and ideas for their tasks at the end of class. The purpose of this activity was to get PSTs to identify a specific goal that each wanted to address and to scaffold their thinking about how to use IGS as a reorganizer to effectively achieve that goal. We wanted PSTs to leave class, which was the final class of the semester, with some direction regarding what their tasks would be about and some ideas that PSTs could use to develop them.
The description and rubrics for this assignment are given as Appendix G. We note that the description of the assignment is almost exactly the same as that given to PSTs when they revised the Intersecting Chords task in groups. Thus, PSTs were able to draw on the work that they had completed in a more scaffolded setting (i.e., revising a task and working with peers) in creating a task of their own. We note, however, the requirement that PSTs create an original task for this assignment. As there are many applets available online, we were concerned that PSTs might find one that addressed the goal that they had in mind and would simply add a few prompts to create the task. This approach to the assignment would bypass the reasoning about the role of IGS in achieving the goals of the task that we wanted PSTs to engage with. That is, we wanted PSTs to use IGS to address specific goals rather than gleaning goals from a given task that used IGS. However, in discussing this requirement of the assignment with PSTs, we did encourage them to look at such preconstructed applets for ideas about how they might use GeoGebra in their task.
The main difference between the descriptions of the assignments for revising the Intersecting Chords task and Designing a Task using IGS is the inclusion of a grading rubric for the latter assignment (see
Appendix G). The purpose of the rubric was to guide PSTs to consider the context for their task and to elicit their thinking and reasoning about their task and how they made use of the IGS Framework in developing it. We asked PSTs to do the following:
Develop a complete task
Develop at least two possible solution strategies for completing the task
Articulate the mathematical goal(s) and students’ prior knowledge
Articulate the goal(s) for students’ mathematical thinking (i.e., one of the rows of the IGS Framework)
Explain how the task they created uses IGS as a reorganizer with respect to the thinking goals, and to reference the IGS Framework in their justification
Each of these aspects of the assignment was given a point value as an indicator of the relative importance of that portion of the assignment. We decided that each task would be evaluated according to the degree that PSTs addressed that aspect of the assignment rather than whether they had successfully created a task that used IGS as a reorganizer along the intended dimension. We reasoned that the assignment needed to be low risk in order for PSTs to have the freedom to develop task in line with their interests and understanding of the IGS Framework, and to continue to grow in their understanding of the role of IGS in supporting students mathematical thinking. In short, we viewed this assignment as a formative assessment, and graded it as such.
Data and Analysis
The data corpus that was analyzed included tasks that each of the 23 PSTs designed for their final project assignment and the rationales that they wrote explaining and justifying how IGS was used as a reorganizer along the dimension that was the target goal for students’ thinking. One teacher was absent during the first week of the intervention and was excluded from the analysis, leaving 22 tasks and rationales. First, the tasks that PSTs created were analyzed to determine (1) if PSTs created a task that used IGS as a reorganizer along the dimension of the IGS Framework they identified as the goal of the task, and (2) whether the task was of high-level cognitive demand. This analysis was conducted to determine whether PSTs could successfully create a high-level task that used IGS as a reorganizer. Following this analysis, PSTs’ rationales for how their tasks used IGS as a reorganizer were analyzed to determine the degree to which PSTs were successful in creating a task that was a reorganizer along the dimension that they intended, and whether their justification articulated sound reasoning about using IGS as a reorganizer. This analysis was aimed at determining the degree to which PSTs’ understanding of the IGS Framework was related to their ability to create a high-level task that used IGS as a reorganizer.
To assess the tasks that PSTs created, each task was analyzed by each of the three authors along each dimension of the IGS Framework to determine whether or not the task used IGS as a reorganizer. At this point in the analysis, no attention was given to which dimension was the target dimension. After each of the 22 tasks was analyzed by all three members of the research team, discrepancies were resolved through discussion of the task in light of the IGS Framework.
To determine the cognitive demand of the task, the Instructional Quality Assessment Toolkit for Mathematics (Matsumura, Garnier, Slater, & Boston 2008; Boston, 2012) was used. Tasks were analyzed using the Academic Rigor rubric, which measures the degree to which students have the opportunity to engage in cognitively challenging mathematical work. The Academic Rigor rubric includes rubrics for the Potential of the Task, the Implementation of the Task, the Rigor of the Discussion, and the Rigor of Teacher’s Questions, the latter three of which are used to assess the Academic Rigor of the task during implementation and discussion. As PSTs did not implement the tasks they had created, only the Academic Rigor rubric for Potential of Task was used for analysis as it is intended measure the potential of a task as written to elicit high-level thinking from students. Each task is scored on a 0–4 point scale, where a 0 represents a task that requires no mathematical activity, a 1 or 2 represents a low-level cognitive demand task, and a 3 or 4 represents a high-level task. Each task was assigned a numerical rating by two of the authors and an outside IQA expert. As the primary concern was whether the task was high level or not, coding discrepancies were defined by a task that received a 1 or 2 by one coder and a 3 or 4 by another. (No tasks received a score of 0.) Using this criterion, there were coding discrepancies for three of the 22 tasks, each of which was resolved through discussion.
Following the analysis of the tasks, the rationales that PSTs generated about their tasks were analyzed. The first concern was whether PSTs created a task that used IGS as a reorganizer with respect to the dimension of the framework that they intended. For example, if the teacher identified the primary goal of the task for students’ thinking as making mathematically meaningful observations and noticing invariances, this goal was cross-checked with the researchers’ analysis of the task that the teacher created to determine whether it used IGS as a reorganizer with respect to this goal. As the goals represented by each dimension of the IGS Framework are discrete but not necessarily mutually exclusive, it was quite common that PSTs created tasks that used IGS as a reorganizer along more than one dimension. This analysis was aimed at determining whether the teacher achieved the target goal.
In addition to asking PSTs to identify the primary goal for students’ thinking that their tasks addressed, the final project also required PSTs to explain how their tasks used IGS as a reorganizer with respect to that goal. For example, if a teacher had identified making mathematically meaningful observations and noticing invariances as the goal for students’ thinking, we would expect some explanation about how the sketch and prompts that they created supported students in achieving that goal. PSTs might explain how the continuous dragging of a figure would reveal an invariant property of the figure that would be difficult to notice in a static environment, and/or how students were guided to reason from the dynamic sketch rather than a static table or figure. The purpose of this analysis was to assess the degree to which PSTs’ understanding of the IGS Framework supported their ability to create tasks that used IGS as a reorganizer with respect to a given dimension. We hypothesized that it was possible for a teacher to create a task that addressed the target dimension without a clear understanding of how, and that doing so would not translate into knowledge or skill that would allow that teacher to create such tasks on a consistent basis. Furthermore, we were interested in how common this phenomenon was. For example, if many PSTs were able to create such a task but were unable to explain how it made use of IGS as a reorganizer along the target dimension in a way that was consistent with the intention of the IGS Framework, we might conclude that the IGS Framework did not effectively support PSTs in creating such tasks.
Two of the authors analyzed each of the rationales associated with the 22 tasks. This analysis was aimed at determining how PSTs’ understanding of the IGS Framework informed the design of the their task as articulated in their written justification of how the task used IGS as a reorganizer with respect to the target goal for students’ thinking. We began by reading the rationales and classifying them as strong or weak, and then we refined this evaluation by examining what features of a teacher’s rationale caused us to classify it the way that we did. In this process, four categories emerged as a way to classify PSTs’ explanations:
1. Evidence of understanding
2. Evidence of partial understanding
3. Evidence of lack of understanding
4. Lack of evidence of understanding
The criterion for the first category, evidence of understanding, was that the explanation provided by the teacher made a clear connection between the description of a reorganizer in the IGS Framework and how the task embodied that description. A key component of this criterion was that the description was specific to the task they had created as opposed to simply repeating the IGS Framework language and claiming that the task fit that description without explaining how. For example, one teacher provided the following description of how the created task supports students in making mathematically meaningful observations and noticing invariance:
The sketch allows for continuous dragging without changing the properties of the quadrilateral and the task prompts students to examine these attributes to draw conclusions. The dynamic aspect of the task truly allows students to recognize what stays the same and what changes as they interact with the quadrilaterals, thus being able to prove invariances.
The teacher’s explanation is related to the specific task that they created, and clearly articulates how it satisfies the description of a reorganizer along this dimension of the IGS Framework.
Evidence of partial understanding generally referred to an explanation that addressed some part, but not all, of the description of a reorganizer in the IGS Framework. For example, a teacher who identified a goal of having students make and test conjectures might note that the prompts explicitly require students to test and refine their conjectures but may not describe how the sketch provides the feedback necessary to do that. As both are needed to use IGS as a reorganizer on this dimension, such an explanation was described as evidence of partial understanding.
An evidence of a lack of understanding was used to describe a situation in which the teacher clearly misinterpreted the intention of the IGS Framework. For example, one teacher claimed that the task required students to drag continuously because it prompted students to drag a quadrilateral from a square to a rectangle, then to a trapezoid, and finally to a general quadrilateral in a “drag and stop” manner. In other words, the purpose of the dragging was simply to create a new figure, not to reveal invariant properties of these shapes. This is a clear misunderstanding of what is meant by “continuous dragging” as described in the first dimension of the IGS Framework.
Finally, there were cases in which PSTs’ descriptions were too general or vague to infer what they did or did not understand about the IGS Framework as it related to the tasks that they created, which we classified a lack of evidence of understanding. This primarily included cases where the language from the IGS Framework was cited, but the description of how the task embodied this description was too general to assess what the teacher did or did not understand about the IGS Framework or how that understanding influenced the design of their task. For example, one teacher provided the following justification for why her task was a reorganizer with respect to making mathematically meaningful observations about similar triangles:
Throughout the tasks, students are focusing on math and making important mathematical connections that will be a foundation of geometry to come. They are able to see how the amount the side lengths change is relative to the amount the shape grew by. They will be able to see how a ratio will affect the shape. Students will also be making the important connection between the slopes of the sides.
We interpret this statement as a claim about the task without supporting evidence in the form of a specific description of how the sketch and prompts support students in making mathematically meaningful observations as it relates to using the dynamic affordances of IGS to uncover specific properties or invariances. She makes specific claims about what students will be able to “see” but does not elaborate as to how continuous dragging and dynamic measurements will support students in making these observations; a similar explanation could be used to justify a task that used triangles constructed on graph paper instead of IGS. As we were unable to determine whether this was due to a superficial understanding, misinterpretation of the framework, or simply the teacher’s failure to support their claim with evidence, we withheld judgment in these cases.
Results
We describe the results first for the analysis of the tasks that PSTs created with respect to whether they used IGS as a reorganizer and whether they were of high cognitive demand. Subsequently, we describe the results for the analysis of PSTs’ rationales in terms of how they supported PSTs in creating their tasks.
Tasks
Of the 22 PSTs, 15 were successful in designing a task that used IGS as a reorganizer with respect to a particular dimension of the framework (68%). Among the seven PSTs who were not, three were secondary and four were elementary, as shown in Table 1. This is noteworthy; although there is nothing expressly written into the framework that connects to a particular topic or grade level of mathematics, the IGS Framework was developed with secondary mathematics instruction in mind. These results demonstrate that elementary PSTs were actually more successful (in terms of percentages) in designing tasks that used IGS as a reorganizer with respect to the target dimension than their secondary counterparts.

With respect to cognitive demand, 21 of the 22 PSTs created tasks that were of high level cognitive demand.1 This is notable as the assignment and rubric did not address the issue of cognitive demand explicitly (i.e., PSTs were not asked to create a high-cognitive demand task), but only the creation of a task that used IGS as a reorganizer along one dimension of the framework. Table 2 shows the relationship between the use of IGS as a reorganizer and the cognitive demand of the task. Examples of tasks from each of the nonempty intersections (reorganizer-high, amplifier-high, and amplifier-low) that PSTs created are provided as
Appendix H.
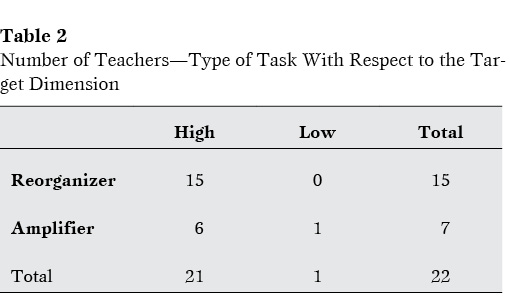
These results corroborate previous findings that the use of technology as a reorganizer was correlated with high-cognitive-demand tasks during setup and implementation (Sherman, 2014). In the present study, these results demonstrate the same finding for tasks as written. Similarly, the same study cited above found that when technology was used as an amplifier, there was variation in the cognitive demand of the task: some tasks were high level and some were low level. Although there is little variation with respect to cognitive demand in the tasks created by these PSTs, it is notable that the only low-level task used IGS as an amplifier. Given that the use of IGS as an amplifier in a task implies that the task could be implemented without the use of technology (i.e., IGS simply makes some of the work involved in the task more efficient or accurate without altering the cognitive focus of the task), it makes sense that the cognitive demand of a task would be independent of the use of IGS in this way.
Rationales
The results regarding the tasks that PSTs created were encouraging: more than two-thirds created tasks that used IGS as a reorganizer in a high-level task. However, with no control group for comparison, we sought a way to determine how the IGS Framework supported PSTs in creating such tasks. Thus, we asked PSTs to articulate their reasoning for how the tasks they designed used IGS as a reorganizer. In particular, we wanted PSTs to make connections between their tasks and the IGS Framework, explaining specifically how their tasks exemplified the description of IGS use as a reorganizer with respect to a particular goal for students’ thinking. Table 3 depicts the results of the analysis of PSTs’ rationales for their tasks.

“Met target dimension” refers to those PSTs who were successful in creating a task that used IGS as a reorganizer with respect to a particular dimension of the IGS Framework that they had identified as the primary goal of the task; “did not meet target dimension” refers to those PSTs who did not. Of the 15 PSTs who did meet the target dimension, 14 wrote rationales that exemplified an understanding of the IGS Framework as it related to their task while the remaining teacher wrote a rationale that did not provide evidence of understanding or of a lack of understanding. On the other hand, of the seven PSTs who did not meet the target dimension, five of them demonstrated a lack of understanding of the IGS Framework, articulated as a misinterpretation or some confusion (see the Analysis section for an example), while the remaining two did not write explanations that provided insight into their understanding of the IGS Framework.
These results support the claim that for these PSTs, an understanding of the IGS Framework supported them in creating a task that used IGS as a reorganizer with respect to a specific goal. On one hand, those PSTs who demonstrated a lack of understanding of the IGS Framework were not successful in creating such tasks. On the other hand, those who demonstrated an understanding of the IGS Framework as it related to the task they designed were successful creating such a task.
Thus, in revisiting our previous hypothesis that it is possible for PSTs to create a task that is a reorganizer for a particular goal within the IGS Framework without a clear understanding of how, our results seem to indicate that this is unlikely. In other words, it appears that an understanding of the IGS Framework facilitates PSTs in articulating their design decisions. And, as previously noted in the literature, design decisions when creating mathematical tasks that utilize technology can support or hinder students’ thinking (Sinclair, 2003). Therefore, our results are encouraging as it is important for PSTs to be able to not only design tasks that target specific goals for students’ thinking but to also be able to articulate how the design choices influence those goals.
Conclusions and Implications
Previous iterations of this intervention with preservice and in-service PSTs in a variety of contexts demonstrated that PSTs were able to use the IGS Framework to effectively evaluate tasks, but this was the first attempt at having PSTs use the IGS Framework to design a task. Based on the results described here, there is reason to be optimistic about PSTs’ ability to make sense of the IGS Framework and effectively utilize it to evaluate, revise, and design tasks that make use of IGS as a reorganizer. Furthermore, the intervention is adaptable enough to be implemented in a variety of contexts.
We provide the tasks that PSTs evaluated and revised during this intervention but have used others in subsequent iterations (after the fourth). Depending on the context in which this intervention would be implemented (e.g., elementary or secondary, content or methods course, preservice or in-service PSTs), a teacher educator may want to select different tasks for PSTs to evaluate and/or revise. The primary criteria we used in selecting tasks for PSTs to evaluate were (1) that it was a task found in, and possibly adapted from, curricular materials that PSTs use or might use, and (2) that the sequence of three tasks increased in complexity. We started with a task that was clearly an amplifier with respect to all three goals according to the IGS Framework, and moved on to tasks that may have varied with respect to the use of IGS for different goals or for which there might be differences regarding how PSTs classified the task depending on what aspect of the task they attended to. This allowed us to build on PSTs growing understanding of the distinctions made in the IGS Framework.
For those interested in implementing this intervention, we emphasize a few important elements that we believe should be included regardless of how it may be adapted. First, we believe that is important for PSTs to engage in these tasks as learners in order to effectively evaluate them using the IGS Framework; looking at the task and imagining what students might do or think about will likely not be sufficient for PSTs to notice the salient aspects of the task in terms of the thinking demands, the use of technology, and how these are related. To this end, we also recommend that PSTs have some familiarity with the IGS that they will use to engage in the task (e.g., GeoGebra, GSP, Cabri). Although mastery is not necessary, if PSTs are using IGS for the first time, it is unlikely that they will be able to reflect on those elements of the task that are relevant to assessing its use of IGS. In our experience, PSTs tend to project their own difficulty using IGS onto how students might engage with the task.
Finally, we believe that it is crucial that some discussion of the task evaluations take place in a whole-class setting in order to address discrepancies. Discrepancies generally occur when PSTs interpret the task prompts differently or interpret the IGS Framework differently. Discrepancies of the first kind highlight how the task prompts are crucial and that clarification by the teacher during implementation may be necessary. For example, if a prompt for students to drag a figure is interpreted as a drag-and-stop action, then a teacher might call the use of IGS an amplifier along the first dimension, and rightly so. But another teacher may interpret the same prompt as calling for continuous dragging and, thus, conclude that IGS is being used as a reorganizer, which would also be consistent with the intention of the IGS Framework. Rather than dissecting the language of the prompt, a teacher educator might highlight how each point of view could be correct depending on the interpretation, and emphasize the role of the teacher in being clear with students about expectations during implementation. On the other hand, if a teacher interprets a drag-and-stop action as a reorganizer use of IGS along the first dimension, the teacher educator would want to correct this misinterpretation of the IGS Framework in order to help PSTs understand how the use of the dynamic affordances of IGS can support students’ thinking in a way that is not possible in a static environment.
One resource available to mathematics teacher educators interested in using this intervention is a concise published description of the IGS Framework, including specific examples of how to use it to evaluate and revise a task (Sherman & Cayton, 2015). We believe that having PSTs read this after their initial exposure to the IGS Framework and evaluation of one or two tasks could help to clarify and deepen their understanding of it. An additional adaptation of the intervention described here would be to move the timeline forward a week or two in the course to provide time to provide feedback and clarification to PSTs, especially to those who seemed to misunderstand or misinterpret the IGS Framework.
For 25 years, NCTM (1991, 2000, 2014) has called for a focus on effective use of technology in the teaching of mathematics. The intervention described in this study presents a pragmatic response to assist PSTs in creating IGS tasks that capitalize on the affordances of this specific technological tool to support students’ mathematical reasoning and sense making. Findings from this intervention show that preservice PSTs have the potential to create interactive geometry tasks that not only focus on supporting students’ thinking but also result in high-level tasks (Smith & Stein, 1998). Furthermore, the IGS Framework served as a critical tool in supporting preservice PSTs as they created these tasks. Specifically, when PSTs focused on creating IGS tasks that were a reorganizer along a specific goal for student thinking from the IGS Framework, they also created high-level tasks. We acknowledge that the IGS Framework focuses on amplifier and reorganizer use of IGS along three specific goals for student learning, which is not an exhaustive list of potential student thinking goals. However, the success of this intervention specifically addresses the dire results from previous research regarding PSTs’ difficulties in selecting high-level tasks for use in their classrooms (Stigler & Hiebert, 2004; Sherman, 2014), providing both a practical tool (IGS Framework) and an outline for mathematics teacher educators to implement with PSTs. This intervention provided preservice PSTs with the opportunity to experience the importance of not only using technology for teaching and learning mathematics but also design decisions and how these decisions impact goals for students’ thinking.
Although the IGS Framework and the learning intervention described in this article focus exclusively on interactive geometry software (e.g., GeoGebra, GSP, Cabri), we believe the combination of the goals for student thinking and amplifier/reorganizer distinction for technology use may be applied to other instructional technologies in mathematics instruction. We hypothesize that the IGS Framework may be applicable to other interactive technologies to evaluate, revise, and design tasks that support students’ high-level thinking. For example, interactive statistical software (e.g., Tinkerplots, Fathom) employ interactive tools that may be dragged and manipulated, providing feedback for students to explore mathematical concepts. These similar features lead us to believe that the IGS Framework might be useful for such technologies. Regardless of the specific instructional technology, the initial focus would need to be the goal for student thinking. Then within the identified goal, one would have to consider the affordances of the instructional technology to describe amplifier and reorganizer uses to support student thinking.
References
Ben-Zvi, D. (2000). Toward understanding the role of technological tools in statistical learning. Mathematical Thinking and Learning, 2(1&2), 127–155.
Boston, M. D. (2012). Assessing instructional quality in mathematics. The Elementary School Journal,113, 76–104.
Boston, M. D., & Smith, M. S. (2009). Transforming secondary mathematics teaching: Increasing the cognitive demands of instructional tasks used in teachers’ classrooms. Journal for Research in Mathematics Education, 40(2), 119–156.
Boswell, L., Larson, R., Stiff, L., & Kanold, T. D. (2012). Larson geometry. Boston, MA: Houghton Mifflin Harcourt.
Cayton, C. (2012). Examining the cognitive demand of tasks in three technology-intensive high school Algebra 1 classrooms. In J. J. Lo & L. Van Zoest (Eds.), Proceedings for the 34th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Kalamazoo, MI.
Charles, R. I., Kennedy, D., Hall, B., Bass, L., Johnson, A., & Murphy, S. J. (2012). Pearson geometry Common Core edition. New York: Pearson.
Hollebrands, K. F., & Dove, A. (2011). Technology as a tool for creating and reasoning about geometry tasks. In T. P. Dick & K. F. Hollebrands (Eds.), Focus in high school mathematics: Technology to support reasoning and sense making (pp. 33–52). Reston, VA: National Council of Teachers of Mathematics.
Hollebrands, K. F., Laborde, C., & StraBer, R. (2008). Technology and the learning of geometry at the secondary level. In M. K. Heid & G. W. Blume (Eds.), Research on technology and the teaching and learning of mathematics: Volume 1 research syntheses (pp. 155–205). Reston, VA: National Council of Teachers of Mathematics.
Lee, H. S., & Hollebrands, K. F. (2008). Preparing to teach mathematics with technology: An integrated approach to developing technological pedagogical content knowledge. Contemporary Issues in Technology and Teacher Education, 8(4), 326–341.
Lee, H. S., Hollebrands, K. F., & Wilson, P. H. (2012). Preparing to teach mathematics with technology: An integrated approach to data analysis and probability (2nd ed.). Dubuque, IA: Kendall Hunt.
Matsumura, L. C., Garnier, H., Slater, S. C., & Boston, M. D. (2008). Toward measuring instructional interactions “at-scale.” Educational Assessment, 13, 267–300.
McCulloch, A. M., Lee, H. S., & Hollebrands, K. F. (2015). Preparing to teach mathematics with technology: An integrated approach to algebra (1st ed.). Raleigh, NC: NC State University. Available at https://ptmt.fi.ncsu.edu
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council Teachers of Mathematics. (2014). Principles to actions: Ensuring mathematical success for all. Reston, VA: Author.
National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common core state standards for mathematics. Washington, DC: Authors.
Pea, R. D. (1985). Beyond amplification: Using the computer to reorganize mental functioning. Educational Psychologist, 20(4), 167–182.
Saxon Publishers. (2011). Saxon geometry. Austin, TX: Houghton Mifflin Harcourt.
Sherman, M. F. (2014). The role of technology in supporting students’ mathematical thinking: Extending the metaphors of amplifier and reorganizer. Contemporary Issues in Technology and Teacher Education, 14(3), 220–46.
Sherman, M. F., & Cayton, C. (2015). Using appropriate tools strategically for instruction. Mathematics Teacher, 109(4), 306–310.
Sherman, M. F., Cayton, C., & Chandler, K. (2015) Supporting teachers using appropriate tools strategically: A practical framework for selecting and revising IGS Tasks. Proceedings for the 37th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. East Lansing, MI.
Sinclair, M. P. (2003). Some implications of the results of a case study for the design of pre-constructed, dynamic geometry sketches and accompanying materials. Educational Studies in Mathematics, 52(3), 289–317.
Smith, M. S., & Stein, M. K. (1998). Selecting and creating mathematical tasks: From research to practice. Mathematics Teaching in the Middle School, 3(5), 344–350.
Stein, M. K., Grover, B. W., & Henningsen, M. A. (1996). Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. American Educational Research Journal, 33(2), 455–488.
Stein, M. K., & Lane, S. (1996). Instructional tasks and the development of student capacity to think and reason: An analysis of the relationship between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.
Stigler, J. W., & Hiebert, J. (2004). Improving mathematics teaching. Educational Leadership, 61(5), 12–17.
Zbiek, R. M., Heid, M. K., Blume, G. W., & Dick, T. P. (2007). Research on technology in mathematics education: The perspective of constructs. In F. K. Lester (Ed.), Second handbook of research in mathematics teaching and learning (pp. 1169–1207). Charlotte, NC: Information Age Publishing.
Authors
Milan F. Sherman, Department of Mathematics and Computer Science, Drake University, Des Moines, IA 50311; [email protected]
Charity Cayton, Department of Mathematics, Science, and Instructional Technology Education, East Carolina University, Greenville, NC 27858; [email protected]
Kayla Chandler, STEM Education Department, North Carolina State University, Raleigh, NC 27606; [email protected]
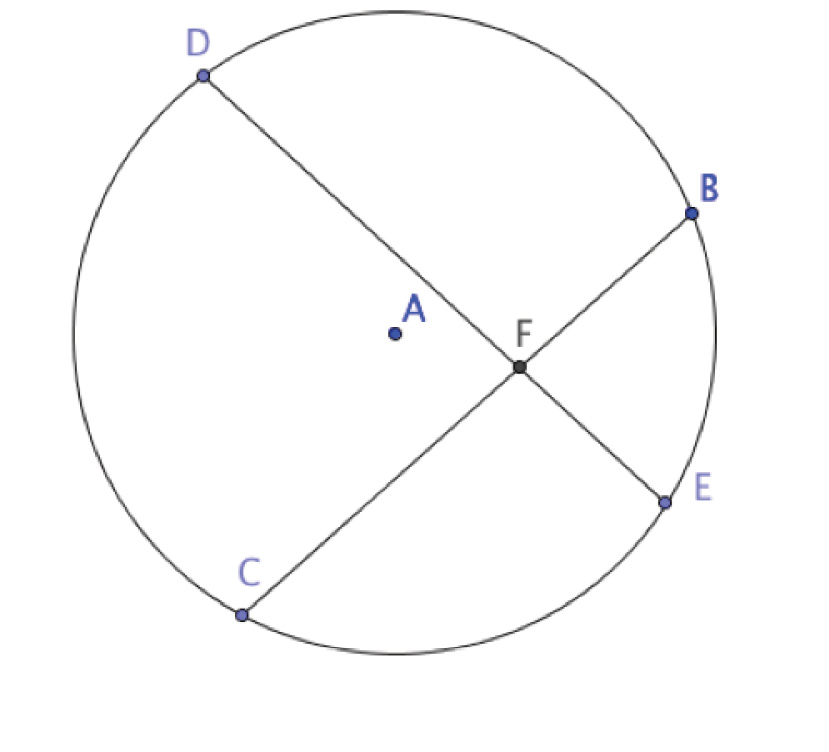
Appendix A: Intersecting Chords Using GeoGebra
(Adapted from Saxon Geometry, Saxon Publishers, 2011)
In this lab, you will use GeoGebra to explore chords and tangents. When two chords intersect in a circle, the segments formed by their intersection have a special relationship.
1. Use the Circle with Center through Point tool to create a circle C.
2. Use the Segment tool to draw two intersecting chords through C. Label them BC and DE.
3. Use the Intersect tool to create the point of intersection, and label it F.
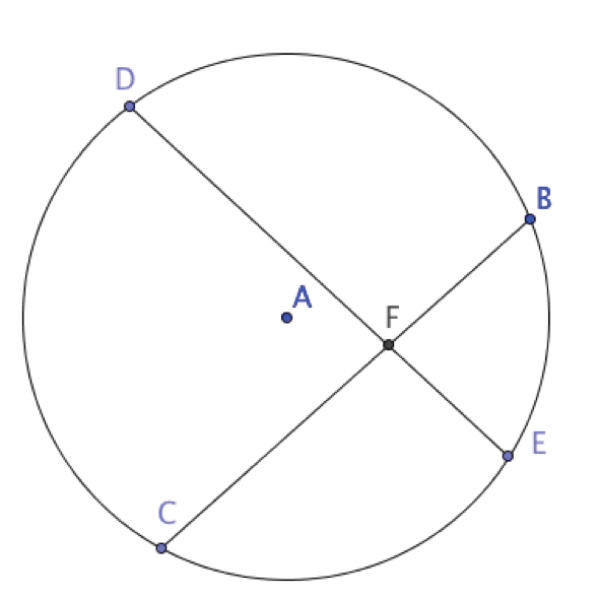
4. Measure the lengths of DF, EF, BF, and CF using the Distance or Length tool.
5. Record the length of each segment in the chart below.
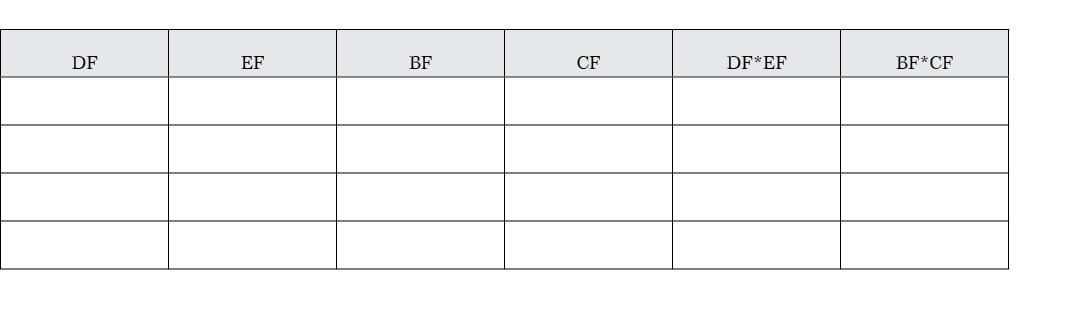
6. Complete the last two columns of the chart by multiplying the indicated segments’ measures and writing their products in the corresponding blanks.
7. Drag your segments to change the length of your chords, and record the new values in the second row of the chart (but make sure they are still intersecting). Repeat this step to fill in the third row of the chart.
8. Using your chart as a guide, what conjecture can you make about the lengths of the segments formed by intersecting chords of a circle?
Appendix B: Exploring Properties of Polygons
(Adapted from Pearson Geometry, 2012)
Use GeoGebra to create a (nonregular) pentagon
,
and extend each side with a ray.
Mark a point on each ray so that you can measure the exterior angles as shown.
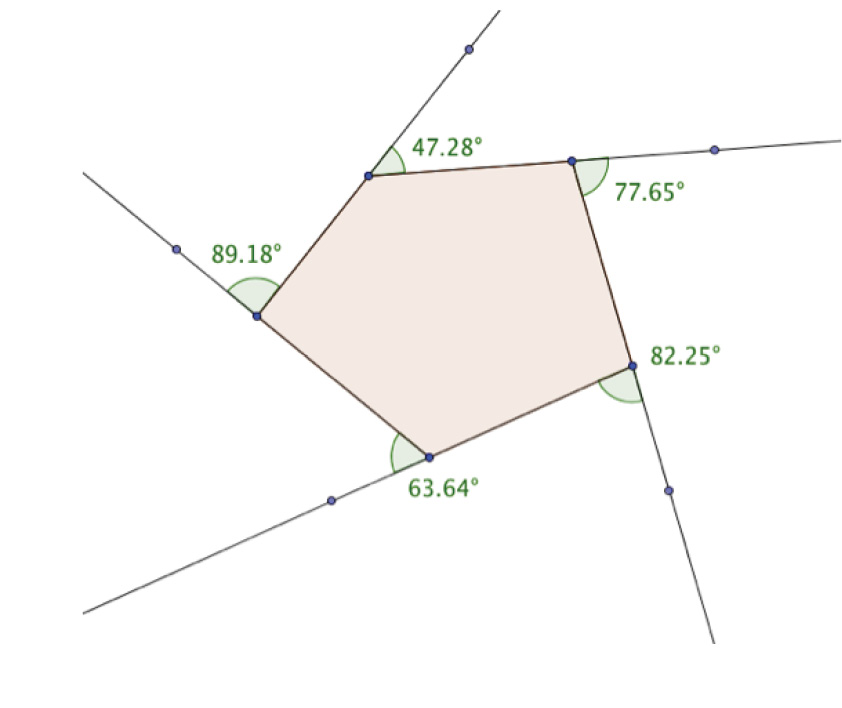
Investigate: Use your figure to explore the properties of a polygon.
• Measure each exterior angle
• Calculate the sum of the measures of the exterior angles.
• Manipulate the polygon. Observe the sum of the measures of the exterior angles of the new polygon.
Exercises
1. Write a conjecture about the sum of the measures of the exterior angles (one at each vertex) of a convex polygon. Test your conjecture with another polygon.
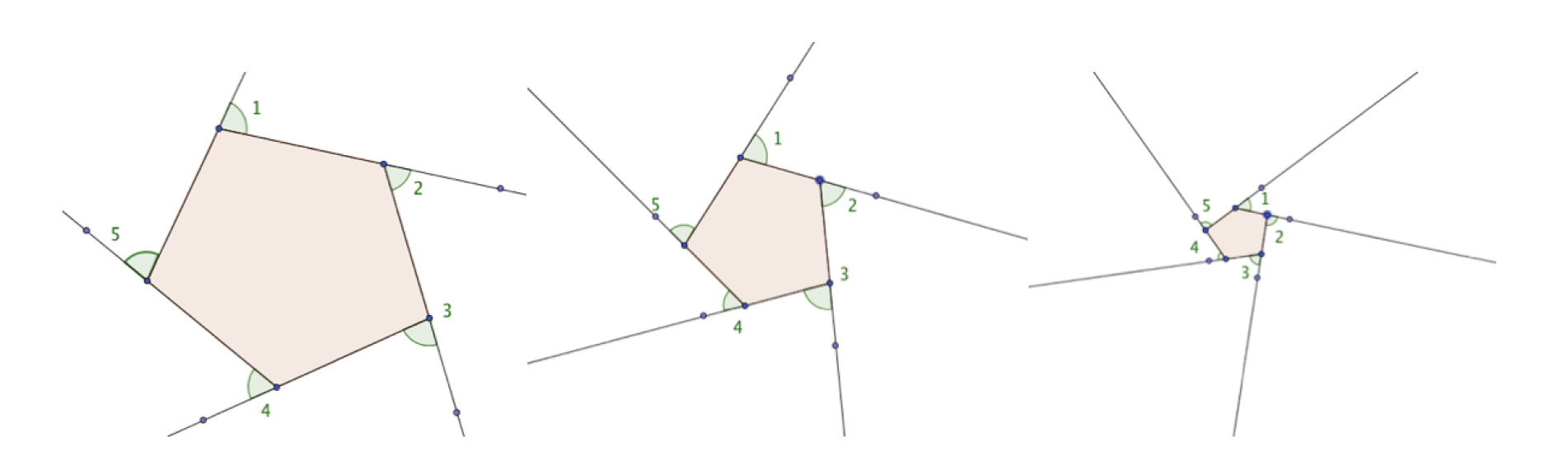
2. Extend: The figures below show a polygon that is decreasing in size until it finally becomes a point. Describe how you could use this to justify your conjecture in Exercise 1.
3. The figure below shows a square that has been copied several times.
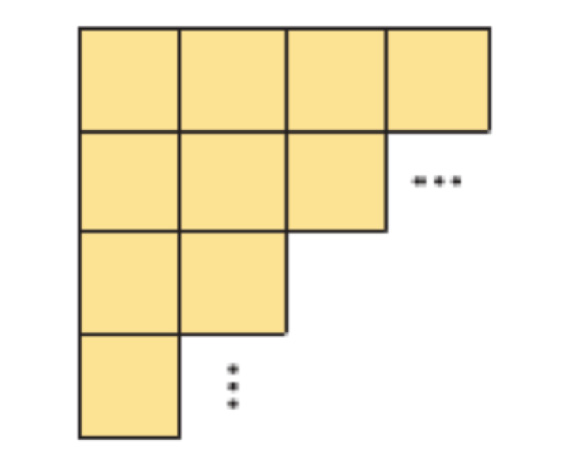
Notice that you can use the square to completely cover, or tile, a plane without gaps or overlaps.
a. Using GeoGebra, make several copies of other regular polygons with 3, 5, 6, and 8 sides. Regular polygons have sides of equal length and angles of equal measure.
b. Which of the polygons that you made can tile a plane?
c. Measure one exterior angle of each polygon (including the square).
d. Write a conjecture about the relationship between the measure of an exterior angle and your ability to tile a plane with the polygon. Test your conjecture with another regular polygon.
Appendix C: Midsegment of a Trapezoid
(Adapted from Holt McDougal Larson Geometry, 2012)
Explore
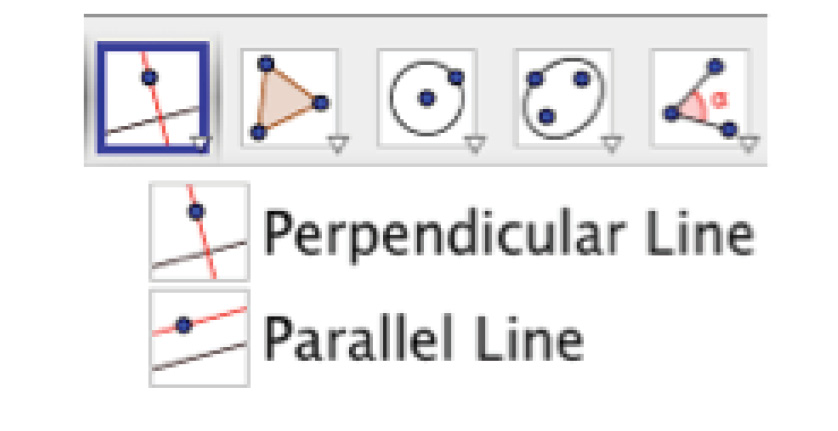
1. Construct line AB and a point C not on AB. Use the Parallel Line tool
to construct a line parallel to AB through C.
2. Construct a point D on the same line as C. Use the Segment tool to draw a segment from A to D and from B to C so that the segments are not parallel, as shown.
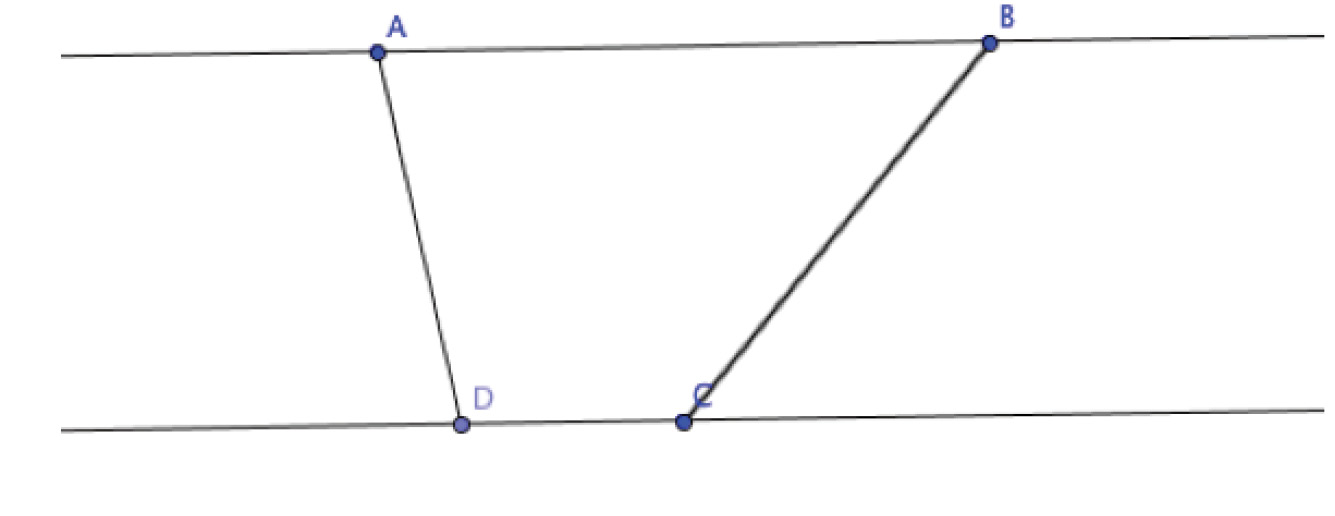
3. Construct the midpoints of segments AD and BC
,
and label them points E and F, respectively. Draw segment EF, which is called the midsegment of trapezoid ABCD. The midsegment of a trapezoid connects the midpoints of its nonparallel sides.
4. Measure segments AB, DC, and EF.
5. The average of AB and DC is AB + DC/2. Calculate and compare this average to EF. What do you notice? Drag point A or point B to change the shape of trapezoid ABCD. Do not allow segment AD to intersect BC. What do you notice about EF and AB + DC/2?
Draw Conclusions
1. Make a conjecture about the length of the midsegment of a trapezoid.
2. The midsegment of a trapezoid is parallel to the two parallel sides of the trapezoid. What measurements could you make to show that the midsegment above is parallel to segments AB and CD? Explain.
3. You have learned a theorem about the midsegment of a triangle. How is the midsegment of a trapezoid similar to the midsegment of a triangle? How is it different?
Appendix D: Overview of the IGS Framework for Teachers





Appendix E: Revising an IGS Task
Choose one of the tasks that you assessed (Midsegment of a Trapezoid or Properties of Polygons), and revise the task along one or two dimensions (rows) for which you assessed it as an amplifier so that GeoGebra is used as a reorganizer in supporting students’ thinking along those dimensions.
Identify the main mathematical goal of the task. That is, what is it that students should understand or be able to do as a result of engaging in the task?
Consider the goal for students’ thinking as represented by a given dimension of the framework:
1. Make mathematically meaningful observations
2. Engage in mathematical exploration
3. Make and test conjectures
How will you revise the task to use GeoGebra to engage students with this thinking while achieving the mathematical goal of the task?
Describe how the revised task uses GeoGebra as a reorganizer to support students’ mathematical thinking as it relates to the goal for students’ thinking. Reference the framework to justify your revisions.
Guidelines
You may change the task as much as you like.
Be sure to address both the sketch and the prompts.
◊ The sketch: How the task makes use of GeoGebra
♦ Will students make the construction or will you create an applet for them to interact with?
♦ Note: Don’t let your knowledge of GeoGebra hinder you—if you have an idea that you don’t know how to implement with GeoGebra, ask me.
◊ The prompts associated with the sketch
♦ What questions will you ask students to think about?
♦ What would students do or say that would indicate that they have achieved the mathematical goal of the task?
♦ What would students do or say that would indicate that they have achieved the thinking goal(s) of the task?
Appendix F: Intersecting Chords Using GeoGebra (Revised)
(Adapted from Saxon Geometry, Saxon Publishers, 2011)
In this lab, you will use GeoGebra to explore chords and tangents. When two chords intersect in a circle, the segments formed by their intersection have a special relationship.
1. Use the Circle with Center through Point tool
to create a circle C.
2. Use the Segment tool
to draw two intersecting chords through C. Label them BC and DE.
3. Use the Intersect tool
to create the point of intersection, and label it F.
4. Measure the lengths of DF, EF, BF, and CF using the Distance or Length tool.
5. Make a conjecture about the relationship between lines DF/EF and BF/CF.
6. How can you prove that your conjecture is true? Can you find an example where it’s not true?
7. Using Geogebra, create another shape that has intersecting segments and test your conjecture for other polygons. How does your conjecture work or not work for other polygons?
8. Using your sketches as a guide, what conjecture can you make about the lengths of the segments formed by intersecting chords of a circle? Intersecting segments of polygons?
Appendix G: Designing an IGS Task
For this assignment you will create a task that uses GeoGebra as a reorganizer in supporting students’ thinking along a dimension described by the IGS Framework.
Identify the main mathematical goal of the task and the grade level that the task is intended for. What is it that students should understand or be able to do as a result of engaging in the task?
Identify the goal for students’ thinking as represented by a given dimension of the framework:
1. Make mathematically meaningful observations
2. Engage in mathematical exploration
3. Make and test conjectures
For this assignment, choose only one goal for students’ thinking that you want to pursue with this task.
Describe how the task you’ve created uses GeoGebra as a reorganizer to support students’ mathematical thinking as it relates to the mathematical goal. Reference the framework to justify how your task accomplishes this.
Guidelines
Your task must be original.
For example, don’t use a pre-constructed applet and simply add some prompts.
You may use curricular or online materials for ideas, but you must create the sketch and prompts that your students will engage with.
The sketch: How the task makes use of GeoGebra
◊ Will students make the construction or will you create an applet for them to interact with?
◊ Note: Don’t let your knowledge of GeoGebra hinder you—if you have an idea that you don’t know how to implement with GeoGebra, ask me.
The prompts associated with the sketch
◊ What questions will you ask students to think about?
◊ What would students do or say that would indicate that they have achieved the mathematical goal of the task?
◊ What would students do or say that would indicate that they have achieved the thinking goal(s) of the task?
Rubric (15 points total)
1. (5 points) A clear, organized, and complete task, i.e., both sketch and prompts, that makes use of GeoGebra and could be implemented with students.
2. (2 points) Complete solutions to the task that include more than one strategy for successfully engaging in the task.
In a separate document, address the following questions about your task. In addition to providing background information about the task and students for whom your task is intended, you will articulate the rationale for your design decisions using the framework.
3. (2 points) Clearly identified mathematical goal, including grade level and necessary prior knowledge.
What should students know, understand, or be able to do as a result of engaging with this task?
What prior knowledge will students need to productively engage with the task and achieve the mathematical goal?
4. (2 points) Clearly identified goal for students’ mathematical thinking and necessary prior knowledge. What type of thinking are students intended to do during this task?
Make mathematically meaningful observations
Engage in mathematical exploration
Make and test conjectures
What prior knowledge or experience will students need to engage in this type of thinking?
5. (4 points) Explain how the task that you’ve created, i.e., both the sketch and the prompts, is a reorganizer with respect the goal for students’ thinking identified in (4) by citing the reorganizer description in the framework.
Explain precisely how students will engage in this sort of thinking while working on the task. For example,
If the goal is to make mathematically meaningful observation or notice invariance, what sort of observations might they make, or what invariances should they discover? How is GeoGebra used to support this goal?
If the goal is to engage in mathematical exploration, what are all the possible ways that students might explore the idea? How does the use of GeoGebra provide alternative paths?
If the goal is to make and test conjectures, what conjectures might students make, and how would they test them? What feedback would the sketch provide to support students?
Appendix H: Examples of Tasks Created by Preservice PSTs
Example 1. A task created with low cognitive demand and amplifier use of IGS on target dimension
Discovering Tangents Using GeoGebra
In this lab, you will use GeoGebra to explore tangents to a circle. When a tangent line is drawn to a point on a circle, the tangent line and the line drawn from the point to the center of the circle have a special relationship.
1. Use the Circle with Center through Point tool to create a circle C.
2. Use the Point on Object tool to add points C and D to the circle you created in step 1.
3. Use the Tangents tool to create tangent lines to points B, C, and D.
4. Use the Segment tool 3 times to draw lines from point A to B, point A to C, and point A to D.
5. Use the Point on Object tool 3 times to add a point on each tangent line.
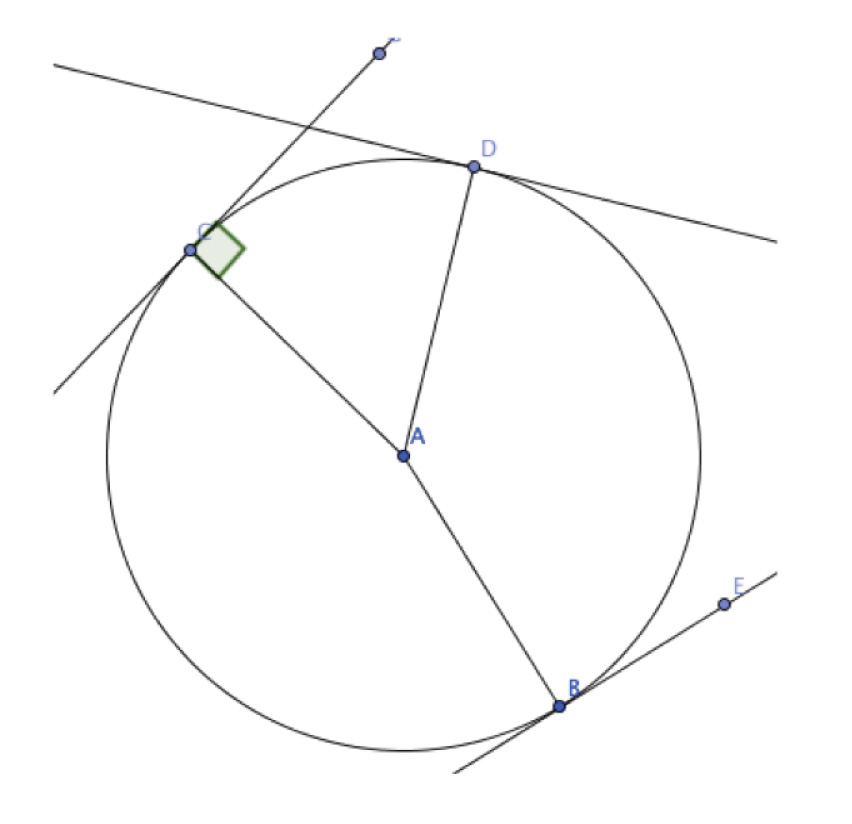
6. Make a conjecture about what you would expect the angles of points B, C, and D to be. Do you think you can make a generalization for all angles of tangent lines based on your conjecture?
7. Use the Angle tool to measure each angle made by each tangent line to the point and the segment from that point to the radius (point A). For example, choose the Angle tool and select the line created by points A and B, and select the tangent line to point B. Was the conjecture you made in step 6 correct?
8. Go back to step 1 and create a new circle. Explore GeoGebra and try to make a generalization that applies to the conjecture you made in step 6.
9. What did you discover? Do you think that this is the same for every circle and its tangents?
Justification for cognitive demand classification
As you can see in the task above, the teacher clearly details what needs to be done to complete this task. Thus, this task received a score of 2 (low cognitive demand) using IQA, indicating that the task is of low cognitive demand since there is little ambiguity about what needs to be done or how to do it.
Justification for evaluation of target dimension
For this task, the teacher’s target dimension for students’ thinking was “Mathematical exploration; use appropriate tools strategically.” However, in this task, the sketch and prompts are guiding students to investigate the same example. Further, freedom with respect to dragging or use of another circle here does not provide alternative paths for students to explore mathematical relationships. Thus, this task uses technology as an amplifier with respect to the target dimension.
Example 2. A task created with high cognitive demand and amplifier use of IGS on target dimension
Area and Perimeter
1. Open the “Graphics” view.
2. Disable the “Axes” and choose “Grid” view in graphics.
3. Choose the “Polygon” tool. (Or use regular polygon tool to make a square.)
4. To draw shapes, put the vertices (corners) on the intersection of the gridlines.
Joe has 36 feet of fencing to make a chicken coop.
1. Joe wants to make his chicken coop a square.
Insert the dimensions of your square.

Joe decides that making his chicken coop a square is not the best idea.
2. He wants to make his chicken coop a rectangle.
Drag the vertices to make new rectangles. Create as many rectangles as you can that have a perimeter of 36 feet. Record below.
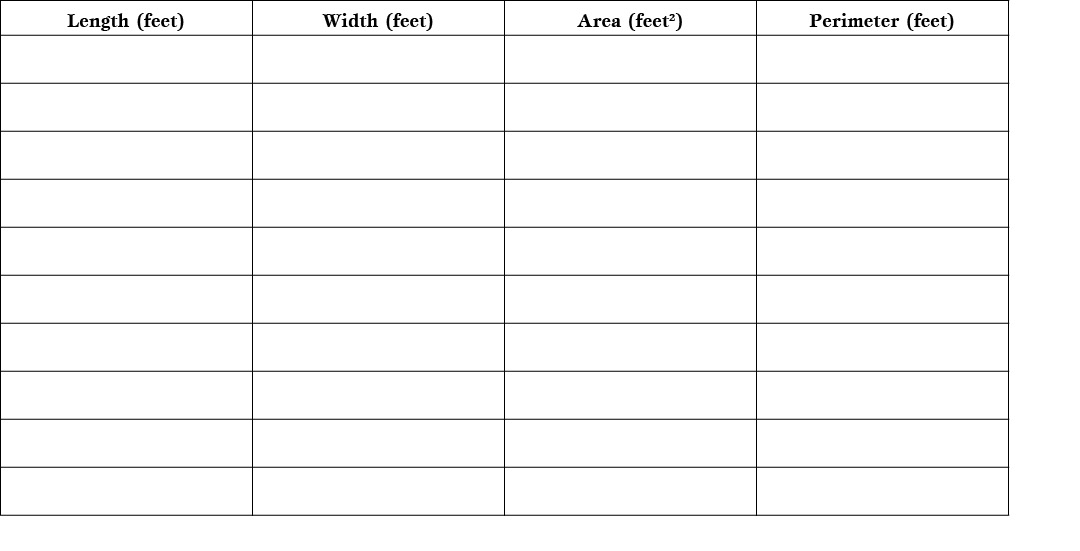
3. Write down any observations you notice from the data in the table.
4. Which chicken coop should Joe build? Why?
5. Which chicken coop has the biggest area?
6. Which chicken coop has the smallest area?
Extension:
1. Create your own word problem that uses area and perimeter of rectangles and squares. Find another friend to give your word problem to, swap, and solve each other’s word problem.
Justification for cognitive demand classification
As you can see in the task above, students will need to complete a table and answer a series of questions related to finding perimeters and areas of rectangles. In answering these questions, students may need to identify patterns, but they are not pressed for generalizations or justifications. Thus, this task received a score of 3 (high cognitive demand) using IQA.
Justification for evaluation of target dimension
For this task, the teacher’s target dimension for students’ thinking was “Make mathematically meaningful observations; look for invariant relationships.” However, in this task, students are dragging with the purpose of creating multiple static examples of rectangles from which to record measurements for a table. Then, students are asked questions that require them to make observations based on the static measurements within the table without reference to the sketch. Thus, this task uses technology as an amplifier with respect to the target dimension.
Example 3. A task created with high cognitive demand and reorganizer use of IGS on target dimension
Analyzing Area of Polygons Using GeoGebra
1. Open the Area of Polygons app provided by the teacher.
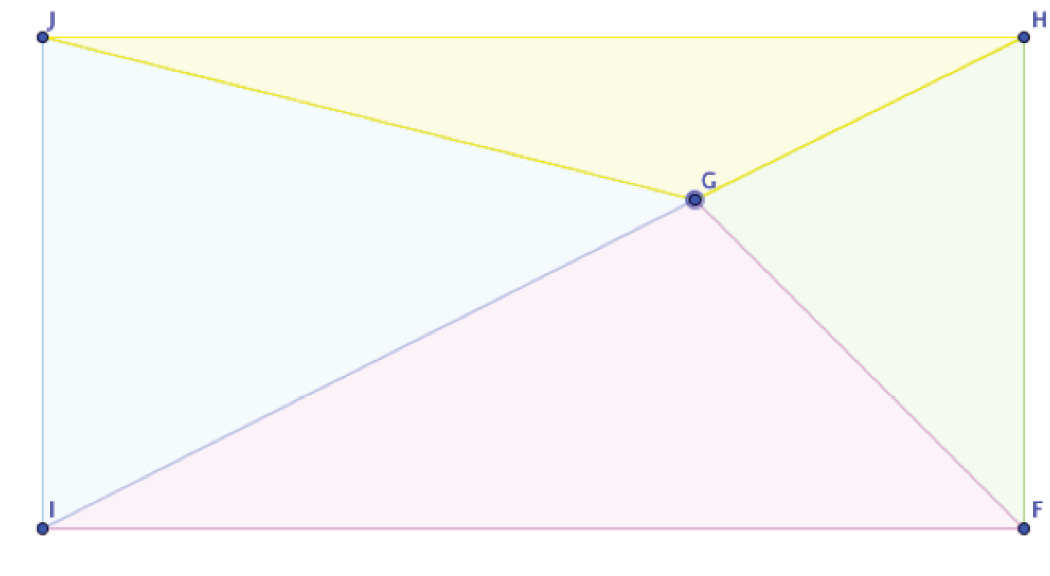
2. Turn on the Algebra View in the top menu bar.
3. Once the Algebra View is turned on, type the following into the Input bar at the bottom of the page:
Multiplication = distance[I,F] * distance[H,F]
This command will give you the area of the Large Polygon.
Multiplication 1 = area[J, H, G], then press Enter
Multiplication 2 = area[H, F, G], then press Enter
Multiplication 3 = area[F, I, G], then press Enter
Multiplication 4 = area[I, J, G], then press Enter
These commands will give you the area for each Small Polygon.
Addition 1 = area [poly2] + area [poly3] + area [poly4] + area [poly5], then press Enter
This command will give you the combined area of the small polygons.
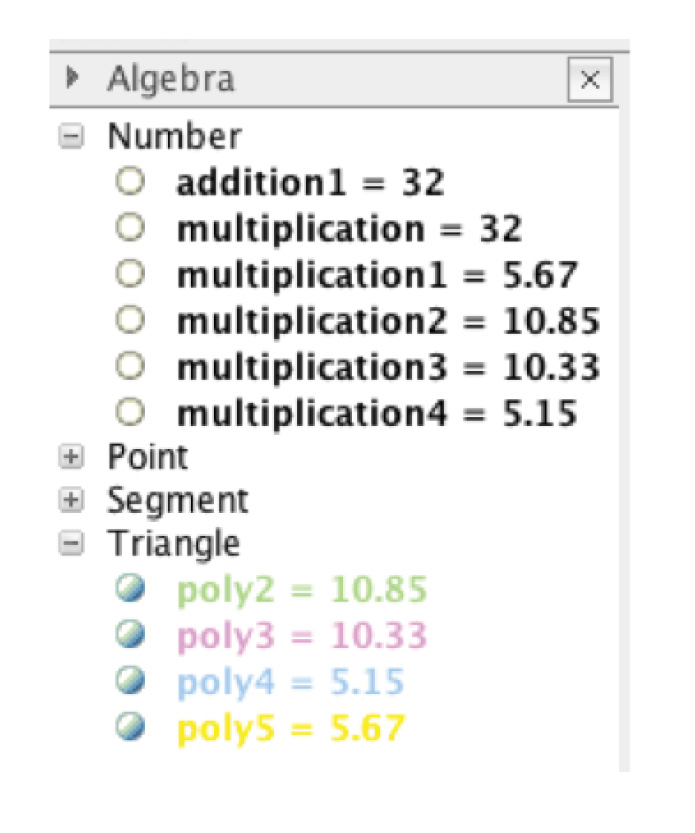
4. Continuously drag point G to change the size (area) of the small polygons and observe any relationships between the areas of the small polygons and the large polygon in the algebra view.
5. Using both the graphics view and the algebra view, what conjecture can you make about the relationship between the areas of the polygons presented?
6. After you have made your conjecture, try to disprove it without altering the properties of the app.
7. Were you able to disprove your conjecture? Why or why not?
Extension: Support your conjecture by adding a 5th point to the larger polygon and observing the relationship between the new areas.
Justification for cognitive demand classification
As you can see in the task above, students are guided to notice relationships between the areas of the small polygons and the large polygon. But, students are not asked to explain or generalize these observations. Thus, this task received a score of 3 (high cognitive demand) using IQA.
Justification for evaluation of target dimension
For this task, the teacher’s target dimension for students’ thinking was “Make mathematically meaningful observations; look for invariant relationships.” In this task, students are dragging with the purpose of examining the relationships between the areas of the various polygons. In prompt 4, the teacher specifically instructs the students to “continuously drag Point G to change the size (area) of the small polygons and observeany relationships between the areas of the small polygons and the large polygon in the algebra view” (emphasis added). Thus, students are expected to make observations by examining the dynamic measurements in the algebra view as point G is dragged. Thus, this task uses technology as a reorganizer with respect to the target dimension.